Class 12 Maths MCQ – Properties of Inverse Trigonometric Functions

This set of Class 12 Maths Chapter 2 Multiple Choice Questions & Answers (MCQs) focuses on “Properties of Inverse Trigonometric Functions”.

1. sin^-1⁡x in terms of cos^-1⁡is ____________
a) cos^-1⁡\(\sqrt{1+x^2}\)
b) cos^-1⁡\(\sqrt{1-x^2}\)
c) cos^-1⁡x
d) cos^-1\(\frac{⁡1}{x}\)
View Answer

2. What is sec^-1⁡x in terms of tan^-1⁡?
a) tan^-1⁡\(\sqrt{1+x^2}\)
b) tan^-1⁡1+x²
c) tan^-1⁡x
d) tan^-1⁡\(\sqrt{x^2-1}\)
View Answer

3. What is the value of cos⁡(tan^-1⁡(\(\frac{4}{5}\)))?
a) \(\frac{5}{4}\)
b) \(\frac{5}{\sqrt{41}}\)
c) \(\frac{\sqrt{41}}{5}\)
d) \(\frac{4}{5}\)
View Answer

Answer: b
Explanation: From ∆ABC, we get

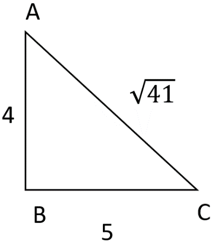
tan^-1⁡(\(\frac{4}{5}\))=cos^-1⁡(\(\frac{5}{\sqrt{41}}\))
cos⁡(tan^-1⁡(\(\frac{4}{5}\))=cos⁡(cos^-1⁡(\(\frac{5}{\sqrt{41}}\)))
=\(\frac{5}{\sqrt{41}}\)

4. What is the solution of cot⁡(sin^-1⁡x)?
a) \(\frac{\sqrt{1-x^2}}{x}\)
b) x
c) \(\sqrt{1-x^2}\)
d) \(\sqrt{1+x^2}\)
View Answer

Answer: a
Explanation: Let sin^-1⁡x=y. From ∆ABC, we get

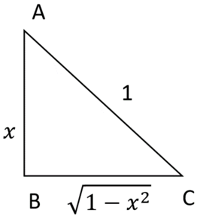
y=sin^-1⁡x=cot^-1⁡(\(\frac{\sqrt{1-x^2}}{x}\))
∴cot⁡(sin^-1⁡x)=\(cot⁡(cot^{-1}(\frac{\sqrt{1-x^2}}{x}))=\frac{\sqrt{1-x^2}}{x}\).

5. Which of the following formula is incorrect?
a) sin^-1⁡x+sin^-1⁡y=sin^-1⁡{\(x\sqrt{1-y^2}+y\sqrt{1-x^2}\)}
b) sin^-1⁡x-sin^-1⁡y=sin^-1⁡{\(x\sqrt{1+y^2}+y\sqrt{1+x^2}\)}
c) 2 tan^-1⁡x=tan^-1⁡\((\frac{2x}{1-x^2})\)
d) 2 cos^-1⁡x=cos^-1⁡(3x-4x³)
View Answer

6. Find the value of sin^-1⁡(\(\frac{5}{13}\))+cos^-1⁡(\(\frac{3}{5}\)).
a) sin^-1⁡(\(\frac{63}{65}\))
b) sin^-1⁡1
c) 0
d) sin^-1⁡(\(\frac{64}{65}\))
View Answer

Answer: a
Explanation: From ∆ABC, we get

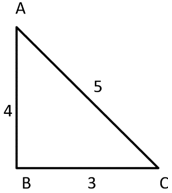
cos^-1⁡\((\frac{3}{5})\)=sin^-1⁡\((\frac{4}{5})\)
∴sin^-1⁡(\(\frac{5}{13}\))+cos^-1⁡(\(\frac{3}{5}\))=sin^-1⁡(\(\frac{5}{13}\))+sin^-1⁡(\(\frac{4}{5}\))
=sin^-1⁡\((\frac{5}{13}\sqrt{1-(\frac{4}{5})^2}+\frac{4}{5}\sqrt{1-(\frac{5}{13})^2})\)
=\(sin^{-1}(\frac{5}{13}×\frac{3}{5}+\frac{4}{5}×\frac{12}{13})=sin^{-1}(\frac{15+48}{65})=sin^{-1}(\frac{63}{65})\).

7. Find the value of tan^-1⁡(\(\frac{1}{3}\))+tan^-1⁡(\(\frac{1}{5}\))+tan^-1⁡(\frac{1}{7})[/latex]
a) tan^-1⁡\((\frac{4}{7})\)
b) tan^-1⁡\((\frac{9}{7})\)
c) tan^-1⁡\((\frac{7}{9})\)
d) tan^-1⁡1
View Answer

8. Find the value of sin^-1⁡(\(\frac{3}{5}\))+sin^-1⁡(\(\frac{4}{5}\))+cos^-1⁡\((\frac{\sqrt{3}}{2})\).
a) \(\frac{π}{3}\)
b) \(\frac{2π}{3}\)
c) \(\frac{4π}{3}\)
d) \(\frac{π}{4}\)
View Answer

9. What is the value of 2 tan^-1⁡x in terms of sin^-1⁡?
a) sec^-1⁡x
b) 2 sec^-1⁡x
c) 2 sec^-1⁡\((\sqrt{1+x^2})\)
d) sec^-1⁡\((\sqrt{1+x^2})\)
View Answer

Answer: c
Explanation: Let 2 tan^-1⁡x=y
⇒tan^-1⁡x=\(\frac{y}{2}\)
From ∆ABC, we get

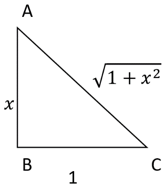
⇒tan^-1⁡x=sec^-1⁡\(\sqrt{1+x^2}=\frac{y}{2}\) ⇒y=2 sec^-1⁡(\(\sqrt{1+x^2}\))

10. sin^-1⁡x+cos¹⁡x= ___
a) \(\frac{π}{2}\)
b) π
c) \(\frac{π}{3}\)
d) 2π
View Answer

Sanfoundry Global Education & Learning Series – Mathematics – Class 12.

To practice all chapters and topics of class 12 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]