Types of Functions - Class 12 Maths MCQ

This set of Class 12 Maths Chapter 1 Multiple Choice Questions & Answers (MCQs) focuses on “Types of Functions”.

1. The following figure depicts which type of function?

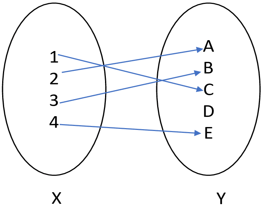
a) one-one
b) onto
c) many-one
d) both one-one and onto
View Answer

Answer: a
Explanation: The above function is one – one. A function f:X→Y is said to be one – one if each of the elements in X has a distinct image in Y.
The condition for a one-one function is for every x₁, x₂ ∈X, f(x₁)=f(x₂)⇒x₁=x₂.

2. The following figure represents which type of function?

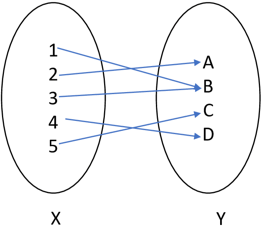
a) one-one
b) onto
c) many-one
d) neither one-one nor onto
View Answer

Answer: b
Explanation: The above function is onto or surjective. A function f:X→Y is said to be surjective or onto if, every element of Y is the image of some elements in X.
The condition for a surjective function is for every y∈Y, there is an element in X such that f(x)=y.

3. A function f∶N→N is defined by f(x)=x²+12. What is the type of function here?
a) bijective
b) surjective
c) injective
d) neither surjective nor injective
View Answer

Answer: c
Explanation: The above function is an injective or one-one function.
Consider f(x₁)=f(x₂)
∴ x₁²+12=x₂²+12
⇒x₁=x₂
Hence, it is an injective function.

4. A function f:R→R is defined by f(x)=5x³-8. The type of function is _________________
a) one -one
b) onto
c) many-one
d) both one-one and onto
View Answer

Answer: c
Explanation: The above is a many -one function.
Consider f(x₁)=f(x₂)
∴5x₁³-8=5x₂³-8
5x₁³=5x₂³
⇒x₁ = ±x₂. Hence, the function is many – one.

5. The function f:R→R defined as f(x)=7x+4 is both one-one and onto.
a) True
b) False
View Answer

Answer: a
Explanation: The given statement is true. f is both one-one and onto.
For one-one: Consider f(x₁)=f(x₂)
∴7x₁+4=7x₂+4
⇒ x₁=x₂.
Thus, f is one – one.
For onto: Now for any real number y which lies in the co- domain R, there exists an element x=(y-4)/7
such that \(f(\frac{y-4}{7}) = 7*(\frac{y-4}{7}) + 4 = y\). Therefore, the function is onto.

Note: Join free Sanfoundry classes at Telegram or Youtube

6. The following figure depicts which type of function?

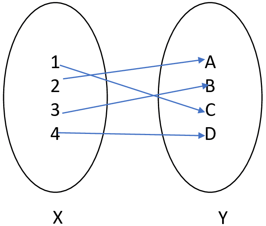
a) injective
b) bijective
c) surjective
d) neither injective nor surjective
View Answer

Answer: b
Explanation: The given function is bijective i.e. both one-one and onto.
one – one : Every element in the domain X has a distinct image in the codomain Y. Thus, the given function is one- one.
onto: Every element in the co- domain Y has a pre- image in the domain X. Thus, the given function is onto.

7. A function f:R→R defined by f(x)=5x⁴+2 is one – one but not onto.
a) True
b) False
View Answer

Answer: b
Explanation: The above statement is false. f is neither one-one nor onto.
For one-one: Consider f(x₁)=f(x₂)
∴ 5x₁⁴+2=5x₂⁴+2
⇒x₁=± x₂.
Hence, the function is not one – one.
For onto: Consider the real number 1 which lies in co- domain R, and let \(x=(\frac{y-2}{5})^{\frac{1}{4}}\).
Clearly, there is no real value of x which lies in the domain R such that f(x)=y.
Therefore, f is not onto as every element lying in the codomain must have a pre- image in the domain.

8. Let A={1,2,3} and B={4,5,6}. Which one of the following functions is bijective?
a) f={(2,4),(2,5),(2,6)}
b) f={(1,5),(2,4),(3,4)}
c) f={(1,4),(1,5),(1,6)}
d) f={(1,4),(2,5),(3,6)}
View Answer

Answer: d
Explanation: f={(1,4),(2,5),(3,6)} is a bijective function.
One-one: It is a one-one function because every element in set A={1,2,3} has a distinct image in set B={4,5,6}.
Onto: It is an onto function as every element in set B={4,5,6} is the image of some element in set A={1,2,3}.
f={(2,4),(2,5),(2,6)} and f={(1,4),(1,5),(1,6)} are many-one onto.
f={(1,5),(2,4),(3,4)} is neither one – one nor onto.

9. Let P={10,20,30} and Q={5,10,15,20}. Which one of the following functions is one – one and not onto?
a) f={(10,5),(10,10),(10,15),(10,20)}
b) f={(10,5),(20,10),(30,15)}
c) f={(20,5),(20,10),(30,10)}
d) f={(10,5),(10,10),(20,15),(30,20)}
View Answer

Answer: b
Explanation: The function f={(10,5),(20,10),(30,15)} is one -one and not onto. The function is one-one because element is set P={10,20,30} has a distinct image in set Q={5,10,15,20}. The function is not onto because every element in set Q={5,10,15,20} does not have a pre-image in set P={10,20,30} (20 does not have a pre-image in set P).
f={(10,5),(10,10),(10,15),(10,20)} and f={(10,5),(10,10),(20,15),(30,20)} are many – one onto.
f={(20,5),(20,10),(30,10)} is neither one – one nor onto.

10. Let M={5,6,7,8} and N={3,4,9,10}. Which one of the following functions is neither one-one nor onto?
a) f={(5,3),(5,4),(6,4),(8,9)}
b) f={(5,3),(6,4),(7,9),(8,10)}
c) f={(5,4),(5,9),(6,3),(7,10),(8,10)}
d) f={(6,4),(7,3),(7,9),(8,10)}
View Answer

Answer: a
Explanation: The function f={(5,3),(5,4),(6,4),(8,9)} is neither one -one nor onto.
The function is not one – one 8 does not have an image in the codomain N and we know that a function can only be one – one if every element in the set M has an image in the codomain N.
A function can be onto only if each element in the co-domain has a pre-image in the domain X. In the function f={(5,3),(5,4),(6,4),(8,9)}, 10 in the co-domain N does not have a pre- image in the domain X.
f={(5,3),(6,4),(7,9),(8,10)} is both one-one and onto.
f={(5,4),(5,9),(6,3),(7,10),(8,10)} and f={(6,4),(7,3),(7,9),(8,10)} are many – one onto.

Sanfoundry Global Education & Learning Series – Mathematics – Class 12.

To practice all chapters and topics of class 12 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Class 12 Maths MCQ – Relations and Functions

» Next - Class 12 Maths MCQ – Composition of Functions and Invertible Function

Related Posts:

Recommended Articles: