This set of Class 12 Maths Chapter 2 Multiple Choice Questions & Answers (MCQs) focuses on “Inverse Trigonometry”.
1. What will be the value of x + y + z if cos-1 x + cos-1 y + cos-1 z = 3π?
a) -1/3
b) 1
c) 3
d) -3
View Answer
Explanation: The equation is cos-1 x + cos-1 y + cos-1 z = 3π
This means cos-1 x = π, cos-1 y = π and cos-1 z = π
This will be only possible when it is in maxima.
As, cos-1 x = π so, x = cos-1 π = -1 similarly, y = z = -1
Therefore, x + y + z = -1 -1 -1
So, x + y + z = -3.
2. Which value is similar to sin-1sin(6 π/7)?
a) sin-1(π/7)
b) cos-1(π/7)
c) sin-1(2π/7)
d) coses-1(π/7)
View Answer
Explanation: sin-1sin(6 π/7)
Now, sin(6 π/7) = sin(π – 6 π/7)
= sin(2π + 6 π/7) = sin(π/7)
= sin(3π – 6 π/7) = sin(20π/7)
= sin(-π – 6 π/7) = sin(-15π/7)
= sin(-2π + 6 π/7) = sin(-8π/7)
= sin(-3π – 6 π/7) = sin(-27π/7)
Therefore, sin-1sin(6 π/7) = sin-1(π/7).
3. What is the value of sin-1(-x) for all x belongs to [-1, 1]?
a) -sin-1(x)
b) sin-1(x)
c) 2sin-1(x)
d) sin-1(-x)/2
View Answer
Explanation: Let, θ = sin-1(-x)
So, -π/2 ≤ θ ≤ π/2
=> -x = sinθ
=> x = -sinθ
=> x = sin(-θ)
Also, -π/2 ≤ -θ ≤ π/2
=> -θ = sin-1(x)
=> θ = -sin-1(x)
So, sin-1(-x) = -sin-1(x)
4. What is the value of sin-1(sin 6)?
a) -2π – 6
b) 2π + 6
c) either -2π + 6 or 2π + 6
d) 2π – 6
View Answer
Explanation: We know that sin(x) = sin(2A * π + x) where A can be positive or negative integer.
If A is -1, then sin(6) = sin(-2π + 6);
If A is 1, then sin(6) = sin(2π + 6);
5. What is the value of cos-1(-x) for all x belongs to [-1, 1]?
a) cos-1(-x)
b) π – cos-1(x)
c) π – cos-1(-x)
d) π + cos-1(x)
View Answer
Explanation: Let, θ = cos-1(-x)
So, 0 ≤ θ ≤ π
=> -x = cosθ
=> x = -cosθ
=> x = cos(-θ)
Also, -π ≤ -θ ≤ 0
So, 0 ≤ π -θ ≤ π
=> -θ = cos-1(x)
=> θ = -cos-1(x)
So, cos-1(x) = π – θ
θ = π – cos-1(x)
=> cos-1(-x) = π – cos-1(x)
6. The given graph is for which equation?
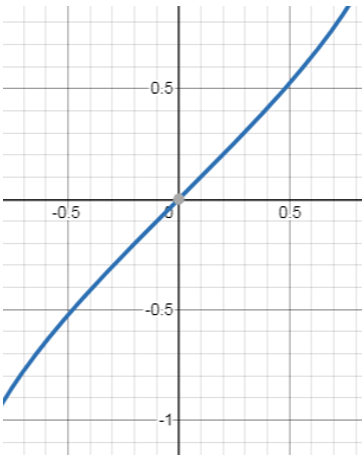
a) y = sinx
b) y = sin-1x
c) y = cosecx
d) y = secx
View Answer
Explanation: The following graph represents 2 equations.
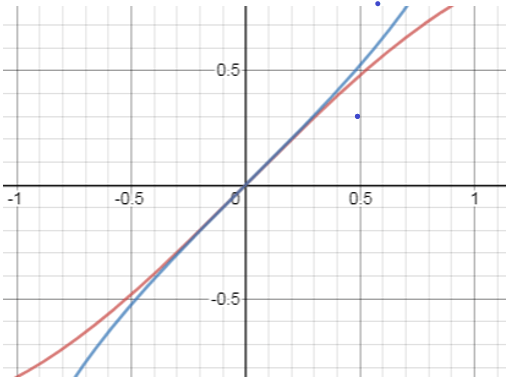
The pink curve is the graph of y = sinx
The blue curve is the graph for y = sin-1x
This curve passes through the origin and approaches to infinity in both positive and negative axes.
7. The given graph is for which equation?
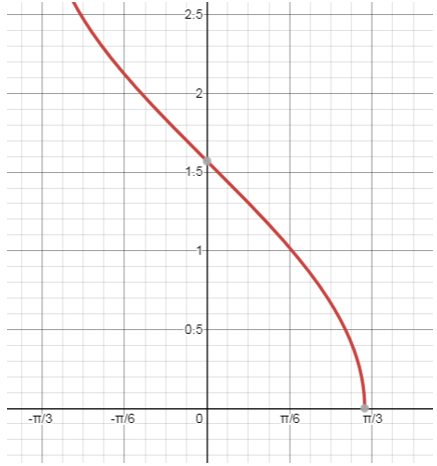
a) cosec-1x
b) secx
c) cos-1x
d) cotx
View Answer
Explanation: There are 2 curves.
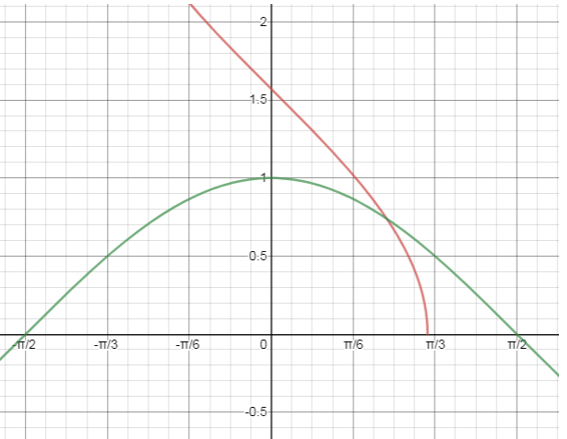
The green curve is the graph of y = cosx
The red curve is the graph for y = cos-1x
This curve origin from some point before π/3 and approaches to infinity in both positive y axis by intersecting at a point near 1.5 in y axis.
8. The given graph is for which equation?
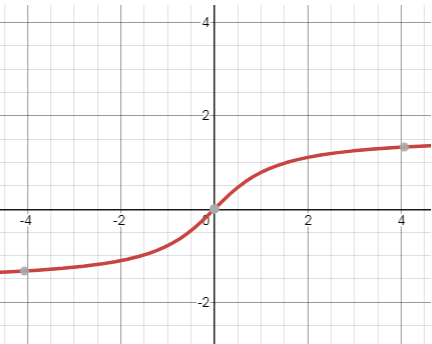
a) y = cos-1x
b) y = cot-1x
c) y = cosec-1x
d) y = tan-1x
View Answer
Explanation: There are 2 curves.
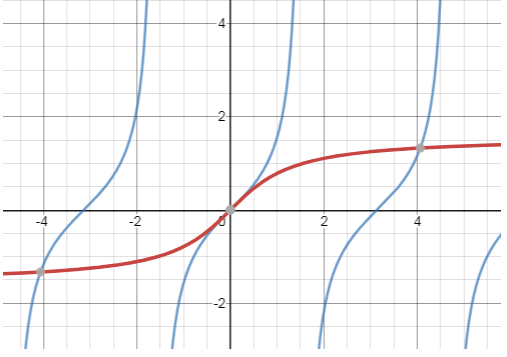
The blue curve is the graph of y = tanx
The red curve is the graph for y = tan-1x
This curve passes through the origin and approaches to infinity in the direction of x axis only.
This graph lies below –x axis and above +x axis.
9. The given graph is for which equation?
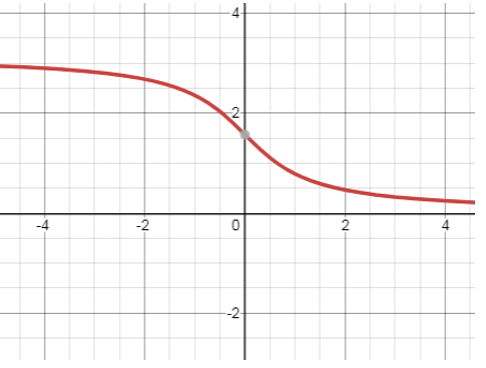
a) y = cot-1x
b) y = tan-1x
c) y = cotx
d) y = cosec-1x
View Answer
Explanation: There are 2 curves.
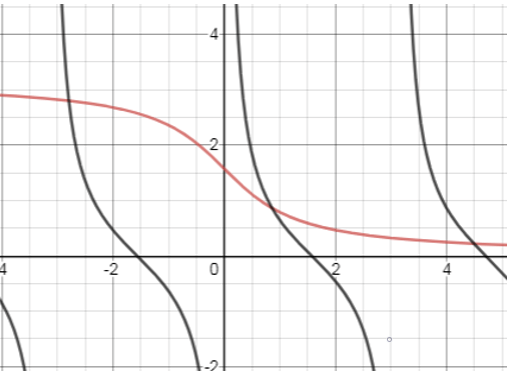
The black curve is the graph of y = cotx
The red curve is the graph for y = cot-1x
This curve does not pass through the origin but approaches to infinity in the direction of x axis only.
The part of the curve that lies in the (x, y) coordinate gradually meets to the x-axis.
This graph lies above +x axis and –x axis.
10. The given graph is for which equation?
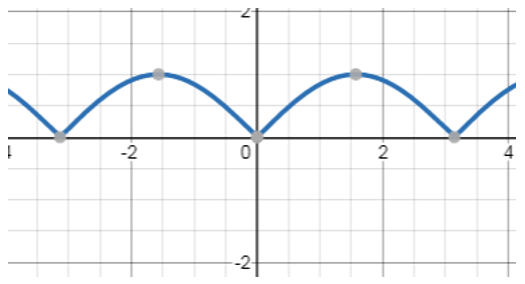
a) y = sinx
b) y = log|sinx|
c) y = |sinx|
d) y = |cosx|
View Answer
Explanation: The given form of equation can be written as,
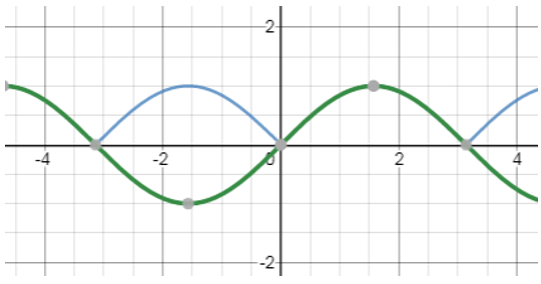
The green curve is the graph of y = sinx
The blue curve is the graph for y = |sinx|
As sinx is enclosed by a modulus so the curve that lies in the negative y axis will come to the positive y axis.
Sanfoundry Global Education & Learning Series – Mathematics – Class 12.
To practice all chapters and topics of class 12 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 12 - Physics MCQs
- Check Class 12 - Mathematics Books
- Practice Class 12 - Biology MCQs
- Practice Class 12 - Chemistry MCQs
- Practice Class 11 - Mathematics MCQs
