This set of Fluid Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Manometer”.
1. In a stationary fluid, how does the local pressure of the fluid vary?
a) With depth only
b) In the horizontal direction only
c) Both with depth and along horizontal direction
d) Neither with depth nor along horizontal direction
View Answer
Explanation: According to Pascal’s law, the local pressure of a fluid is same in all directions. Hence, the pressure won’t vary along the x and y direction. The local pressure will increase with an increase in depth due to the extra weight of water column above that point.
2. Which of the following cannot be the value of absolute pressure of a fluid at any point?
a) 0
b) 1.013 bar
c) – 1 bar
d) 200 bar
View Answer
Explanation: Absolute zero pressure is the reference used for the measurement of absolute pressure. Absolute zero pressure is possible (theoretically). Hence, 0 and positive values are possible, but a negative value is impossible.
3. A student wants to find the absolute pressure of water at a point below the surface of water. He has a barometer and a manometer pressure gauge. The barometer reads 1.3152 bar where as the manometer pressure gauge reads 0.3152 bar. What is the absolute pressure? (Assume that pressure at one end of the manometer is atmospheric.)
a) 1 bar
b) 1.6304 bar
c) 0.3152 bar
d) 1.3152 bar
View Answer
Explanation: The options may tempt you to subtract the readings, but the concept of barometer and manometer is important. Barometer measures the atmospheric pressure whereas, the manometer reads the gauge pressure. Hence, we need to add the two values.
4. In a U-tube manometer, one end is open to the atmosphere, the other end attached to a pressurized gas of gauge pressure 40 kPa. The height of the fluid column in the atmospheric side is 60 cm, and that on the gas side is 30 cm. The manometic fluid used is: (Take g = 9.8 m/s2).
a) Water
b) Liquid ammonia
c) Oil
d) Mercury
View Answer
Explanation: Gauge pressure = 40000 Pa. Height difference = 60 – 30 = 30 cm = 0.3 m. ρ*g*(h2 – h1) = 40000. We get, ρ = 13605 kg/m3 = Density of mercury.
5. In a U-tube mercury manometer, one end is exposed to the atmosphere and the other end is connected to a pressurized gas. The gauge pressure of the gas is found to be 40 kPa. Now, we change the manometric fluid to water. The height difference changes by: (ρmercury = 13600 kg/m3, ρwater = 1000 kg/m3).
a) 1260%
b) 92.64 %
c) Remains unchanged (0%)
d) 13.6%
View Answer
Explanation: Since the gauge pressure remains the same ρ*(h2 – h1) = constant. The height difference in mercury manometer is 0.30 m and that in a water manometer is 4.08 m. Percent change is thus, 1260%. Be careful about the denominator used for computing percent change.
6. A manometric liquid should suitably have _________
a) Low density & Low Vapour pressure
b) Low density & High Vapour pressure
c) High density & Low Vapour pressure
d) High density & High Vapour pressure
View Answer
Explanation: A high density is favourable because the height of the column required for the manometer would be low. A liquid with high vapour pressure would be less sensitive to changes in pressure and may result in a slower rise of the manometric fluid. Thus, a fluid with low vapour pressure is favourable.
7. A simple U-tube manometer can measure negative gauge pressures.
a) True
b) False
View Answer
Explanation: The height of the manometric fluid in a U-tube manometer in the test column would fall if there is a positive gauge pressure. The height would increase if there is a negative gauge pressure. It is possible to measure negative gauge pressures with a U-tube manometer. However, the negative pressure cannot fall below -1 Bar.
8. Both ends of a U-tube manometer are exposed to the atmosphere. There exists a possibility that the height difference of the manometer is non-zero. True or False?
a) True
b) False
View Answer
Explanation: The height difference may be non-zero when there are multiple immiscible fluids used in the same manometer. Even though the pressure is same on both surfaces, the height would be different as the fluid with higher density will be at a lower height.
9.The below figure shows an inclined U-tube mercury manometer. The vertical end of the tube is exposed to a gas of gauge pressure 50 kPa and the inclined end is exposed to the atmosphere. The inclined part of the tube is at an angle of 30o with the horizontal. Find the value of h (in cm) (take g = 9.8 m/s2, ρmercury = 13600 kg/m3)
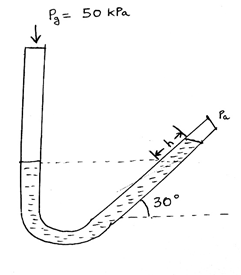
a) 60
b) 50
c) 75
d) 25
View Answer
Explanation: Pressure along the dotted line will be 50 kPa. Gauge pressure in an inclined manometer is given by P = ρ.g.h.sin (Ɵ). Substituting P, ρ and Ɵ, we get the value of h as 0.75 m.
10. In the manometer given above, 2 immiscible fluids mercury (ρ = 13600 kg/m3) and water (ρ = 1000 kg/m3) are used as manometric fluids. The water end is exposed to atmosphere (100 kPa) and the mercury end is exposed to a gas. At this position, the interface between the fluids is at the bottom most point of the manometer. Ignore the width of the manometer tube and the radius of curvature. The value of h is found to be 9.45 m. The height of the mercury column is given to be 75 cm. Find the gauge pressure of the gas. (g = 9.8 m/s2)
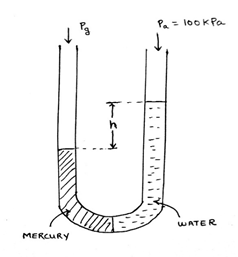
a) 100 kPa
b) 50 kPa
c) 200 kPa
d) 0 kPa
View Answer
Explanation: Height of water column = 0.75 + 9.45 = 10.2 m. We equate the pressures at the bottom most point. Pa + ρw.g.(10.2) = Pg + ρm.g.(0.75). We find, Pg = 100 kPa = Absolute pressure. Hence, gauge pressure will be 0.
Sanfoundry Global Education & Learning Series – Fluid Mechanics.
To practice all areas of Fluid Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Mechanical Engineering Internship
- Apply for Aerospace Engineering Internship
- Practice Aerospace Engineering MCQs
- Check Aerospace Engineering Books
- Check Mechanical Engineering Books
