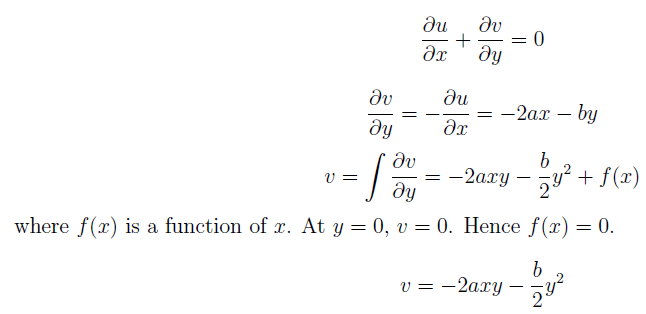Fluid Mechanics Questions and Answers – Continuity Equation

This set of Fluid Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Continuity Equation”.

1. If a liquid enters a pipe of diameter d with a velocity v, what will it’s velocity at the exit if the diameter reduces to 0.5d?
a) v
b) 0.5v
c) 2v
d) 4v
View Answer

Answer: d
Explanation: According to the Continuity Equation,

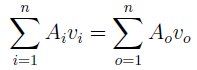
where a represents flow area, v represents flow velocity, i is for inlet conditions and o is for outlet conditions.

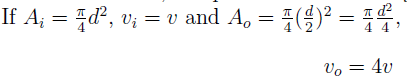
2. The continuity equation is based on the principle of
a) conservation of mass
b) conservation of momentum
c) conservation of energy
d) conservation of force
View Answer

3. Two pipes of diameters d1 and d2 converge to form a pipe of diameter d. If the liquid flows with a velocity of v1 and v2 in the two pipes, what will be the flow velocity in the third pipe?
a) \(\frac{d_1v_1+d_2v_2}{d}\)
b) \(\frac{d^2(v_1+v_2)}{d}\)
c) \(\frac{(d_1+d_2)^2(v_1+v_2)}{d^2}\)
d) \(\frac{d_1^2 v_1 + d_2^2 v_2}{d^2}\)
View Answer

Answer: d
Explanation: According to the Continuity Equation,

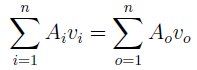
where a represents flow area, v represents flow velocity, i is for inlet conditions and o is for outlet conditions. Thus,

4. Two pipes of diameters d1 and d2 converge to form a pipe of diameter 2d. If the liquid flows with a velocity of v1 and v2 in the two pipes, what will be the flow velocity in the third pipe?
a) v1 + v2
b) v1 + v2/2
c) v1 + v2/4
d) 2(v1 + v2)
View Answer

Answer: c
Explanation: According to the Continuity Equation,

where a represents flow area, v represents flow velocity, i is for inlet conditions and o is for outlet conditions. Thus,

5. Two pipes, each of diameter d, converge to form a pipe of diameter D. What should be the relation between d and D such that the flow velocity in the third pipe becomes double of that in each of the two pipes?
a) D = d
b) D = 2d
c) D = 3d
d) D = 4d
View Answer

Answer: a
Explanation: According to the Continuity Equation,

where a represents flow area, v represents flow velocity, i is for inlet conditions and o is for outlet conditions. Thus,
A₁v₁ + A₂v₂ = Av
d²v + d²v = D²v
D = d.

6. Two pipes, each of diameter d, converge to form a pipe of diameter D. What should be the
relation between d and D such that the
ow velocity in the third pipe becomes half of that in each
of the two pipes?
a) D = d/2
b) D = d/3
c) D = d/4
d) D = d/5
View Answer

Answer: a
Explanation: According to the Continuity Equation,

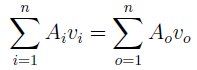
where a represents flow area, v represents flow velocity, i is for inlet conditions and o is for outlet conditions. Thus,
A₁v₁ + A₂v₂ = Av
d²v + d²v = D^v/2
d = D ⁄ 4.

7. In a two dimensional flow, the component of the velocity along the X-axis is u = ax² + bxy + cy².
If v = 0 at y = 0, what will be the velocity component in the Y-direction?
a) v = 2axy + by²
b) v = 2axy + b ⁄ 2 y²
c) v = -2axy – b ⁄ 2 y²
d) v = -axy – b ⁄ 2 y²
View Answer

Answer: c
Explanation: According to the condition for continuity,

8. In a two dimensional flow, the component of the velocity along the X-axis and the Y-axis are u = ax² + bxy + cy² and v = cxy. What should be the condition for the flow field to be continuous?
a) a + c = 0
b) b + c = 0
c) 2a + c = 0
d) 2b + c = 0
View Answer

Answer: c
Explanation: According to the condition for continuity,

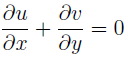
2ax + cx = 0
2a + c = 0.

9. In a two dimensional flow, the component of the velocity along the X-axis and the Y-axis are u = axy and v = bx² + cy². What should be the condition for the flow field to be continuous?
a) a + b = 0
b) a + c = 0
c) a + 2b = 0
d) a + 2c = 0
View Answer

Answer: d
Explanation: The condition for the flow field to be continuous is:

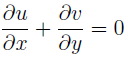
ay + 2cy = 0
a + 2c = 0.

10. In a two dimensional flow, the component of the velocity along the X-axis and the Y-axis are u = ax² + bxy and v = cxy +dy². What should be the condition for the flow field to be continuous?
a) (a + b)x + (c + d)y = 0
b) (a + c)x + (b + d)y = 0
c) (2a + b)x + (c + 2d)y = 0
d) (2a + c)x + (b + 2d)y = 0
View Answer

Answer: d
Explanation: The condition for the flow field to be continuous is:

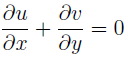
2ax + cx + by + 2dy = 0
(2a + c)x + (b + 2d)y = 0.

11. In a two dimensional flow, the component of the velocity along the X-axis and the Y-axis are u = ax² + bxy and v = bxy + ay². The condition for the flow field to be continuous is
a) independent of the constants (a; b) but dependent on the variables (x; y)
b) independent of the variables (x; y) but dependent on the constants (a; b)
c) independent of both the constants (a; b) and the variables (x; y)
d) dependent on both the constants (a; b) and the variables (x; y)
View Answer

Answer: a
Explanation: The condition for the flow field to be continuous is:

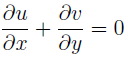
2ax + by + 2ay + bx = 0
x + y = 0
Hence, the condition for the flow field to be continuous is independent of the constants (a; b) and dependent only on the variables (x; y).

12. In a two dimensional flow, the component of the velocity along the X-axis and the Y-axis are u = ax + by and v = ax – by. For what condition will the flow field be continuous?
a) impossible
b) possible if a = b
c) possible if a = 2b
d) possible for all values of a and b
View Answer

Answer: d
Explanation: The condition for the flow field to be continuous is:

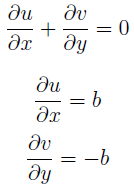
Thus, the condition will be satisfied for any and every value of a and b.

13. In a two dimensional flow, the component of the velocity along the X-axis and the Y-axis are u = ay² + bxy and v = ax² + bxy. The flow will be continuous if
a) a + b = 0
b) a – b = 0
c) x + y = 0
d) x – y = 0
View Answer

Answer: c
Explanation: The condition for the flow field to be continuous is:

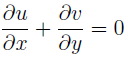
by + bx = 0
x + y = 0.

14. In a two dimensional flow, the component of the velocity along the X-axis and the Y-axis are u = ax² + bxy and v = bxy + ay². The condition for the flow field to be continuous is
a) independent of a and b
b) independent of a and c
c) independent of b and c
d) independent of a, b and c
View Answer

Answer: d
Explanation: The condition for the flow field to be continuous is:

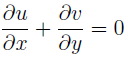
2ax + by + 2ay + bx = 0
x + y = 0
Hence, the condition for the flow field to be continuous is independent of a, b and c.

15. In a water supply system, water flows in from pipes 1 and 2 and goes out from pipes 3 and 4 as shown. If all the pipes have the same diameter, which of the following must be correct?

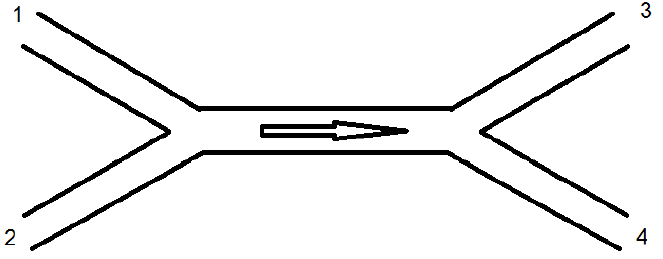
a) the sum of the flow velocities in 1 and 2 is equal to that in 3 and 4
b) the sum of the flow velocities in 1 and 3 is equal to that in 2 and 4
c) the sum of the flow velocities in 1 and 4 is equal to that in 2 and 3
d) the flow velocities in 1 and 2 is equal to that in 3 and 4
View Answer

Answer: a
Explanation: According to the Continuity Equation,

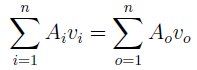
where a represents flow area, v represents flow velocity, i is for inlet conditions and o is for outlet conditions.
A₁v₁ + A₂v₂ = A₃v₃ + A₄v₄
Since d₁ = d₂ = d₃ = d₄, v₁ + v₂ = v₃ + v₄.

Sanfoundry Global Education & Learning Series – Fluid Mechanics.

To practice all areas of Fluid Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]