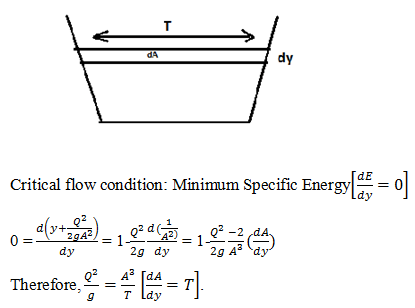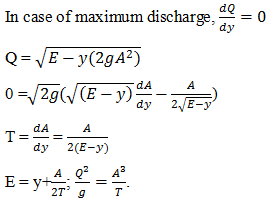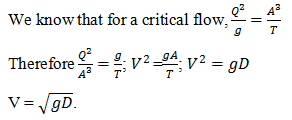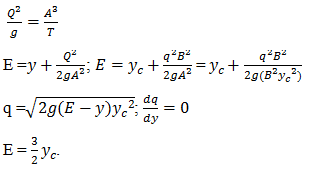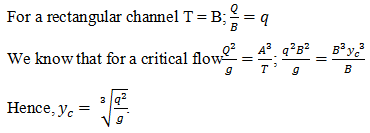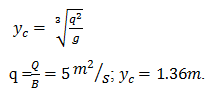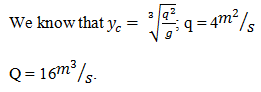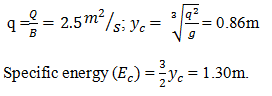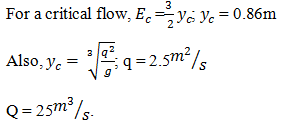Fluid Mechanics Questions and Answers – Critical Flow in Different Channel Sections – 1

This set of Fluid Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Critical Flow in Different Channel Sections – 1”.

1. What is the condition for critical flow?
a) \(\frac{Q}{g} = \frac{A}{T}\)
b) \(\frac{Q^2}{g} = \frac{A^2}{T}\)
c) \(\frac{Q}{g} = \frac{A^3}{T}\)
d) \(\frac{Q^2}{g} = \frac{A^3}{T}\)
View Answer

Answer: d
Explanation:

2. What is the condition for critical flow in case of maximum discharge?
a) \(\frac{Q}{g} = \frac{A}{T}\)
b) \(\frac{Q^2}{g} = \frac{A^2}{T}\)
c) \(\frac{Q}{g} = \frac{A^3}{T}\)
d) \(\frac{Q^2}{g} = \frac{A^3}{T}\)
View Answer

Answer: d
Explanation:

3. Determine the velocity in case of critical flow having top width T and area A.
a) V = gD
b) V = \(\sqrt{gD}\)
c) V = gD²
d) V = g \(\frac{D}{2}\)
View Answer

Answer: b
Explanation:

4. Calculate the specific energy in case of rectangular channel having discharge Q and y_c is the critical depth
a) E = \(\frac{y_c}{2}\)
b) E = \(\frac{3}{2}\) y_c
c) E = 2y_c
d) E = 3y_c
View Answer

Answer: b
Explanation:

5. Estimate the critical depth in case of a rectangular channel having usual dimensions.
a) y_c = \(\sqrt{\frac{q^2}{g}}\)
b) y_c = \(\sqrt[3]{\frac{q^2}{g}}\)
c) y_c = \(\sqrt{\frac{q}{g}}\)
d) y_c = \(\sqrt[3]{\frac{q}{g}}\)
View Answer

Answer: b
Explanation:

6. Calculate the critical depth of a rectangular channel having width 3m and the discharge through it is 15 m³/s.
a) 0.36m
b) 1.36m
c) 2.36m
d) 3.36m
View Answer

Answer: b
Explanation:

7. Calculate the total discharge through a rectangular channel having critical depth of 1.18m and the base width of the channel is 4m.
a) 16 m³/s
b) 20 m³/s
c) 24 m³/s
d) 28 m³/s
View Answer

Answer: a
Explanation:

8. Calculate the minimum specific energy of a rectangular channel having critical depth of 1.5m.
a) 3.25m
b) 2.25m
c) 1.25m
d) 0.25m
View Answer

9. The base width of a rectangular channel is 4m and the maximum discharge through the channel is 10 m3/s, calculate the specific energy.
a) 0.7m
b) 1.0m
c) 1.3m
d) 1.6m
View Answer

Answer: c
Explanation:

10. The minimum specific energy of a rectangular channel is 1.3m and the base width of the channel is 10m, calculate the discharge through the channel.
a) 10 m³/s
b) 15 m³/s
c) 20m³/s
d) 25m³/s
View Answer

Answer: d
Explanation:

Sanfoundry Global Education & Learning Series – Fluid Mechanics.

To practice all areas of Fluid Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]