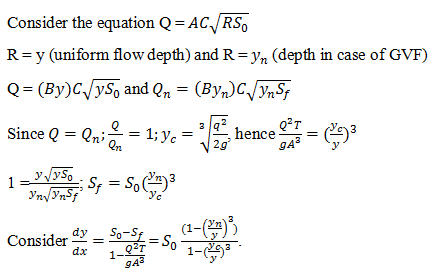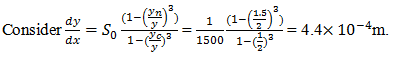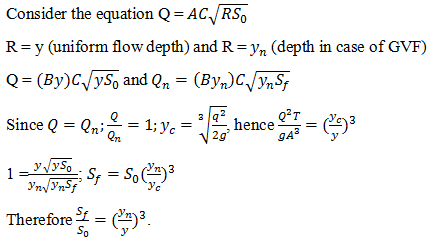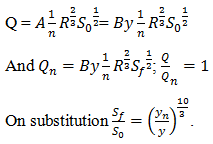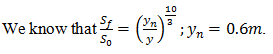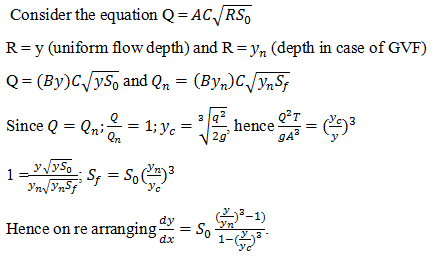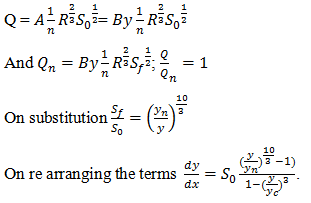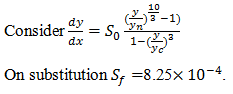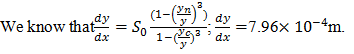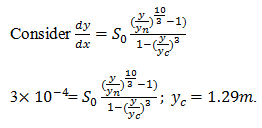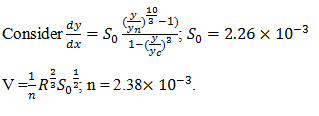Fluid Mechanics Questions and Answers – Gradually Varied Flow in Wide Rectangular Channels

This set of Fluid Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Gradually Varied Flow in Wide Rectangular Channels”.

1. What is the hydraulic radius for a wide rectangular channel section?
a) 3y
b) 2y
c) y
d) y/2
View Answer

2. Which of the following equations is true for a wide rectangular channel?
a) \(\frac{dy}{dx} = S_0 \frac{(1-(\frac{y}{y_n})^3)}{1-(\frac{y}{y_c})^3}\)
b) \(\frac{dy}{dx} = S_0 \frac{(1-(\frac{y}{y_n})^3)}{1-(\frac{y_c}{y})^3}\)
c) \(\frac{dy}{dx} = S_0 \frac{(1-(\frac{y_n}{y})^3)}{1-(\frac{y_c}{y})^3}\)
d) \(\frac{dy}{dx} = S_0 \frac{(1-(\frac{y_n}{y})^3)}{1-(\frac{y}{y_c})^3}\)
View Answer

Answer: c
Explanation:

3. Calculate the rate of change of depth of a wide rectangular channel having uniform flow depth of 2m and the depth during GVF is 1.5m. Given:y_c=1m, S₀=1 in 1500.
a) 1.4×10^-4m
b) 2.4×10^-4m
c) 3.4×10^-4m
d) 4.4×10^-4m
View Answer

Answer: d
Explanation:

4. Which of the following equations is true considering Chezy’s equation?
a) \(\frac{S_0}{S_f} = (\frac{y_n}{y})^3\)
b) \(\frac{S_0}{S_f} = (\frac{y}{y_n})^3\)
c) \(\frac{S_f}{S_0} = (\frac{y_n}{y})^3\)
d) \(\frac{S_f}{S_0} = (\frac{y_n}{y})^3\)
View Answer

Answer: c
Explanation:

5. Which of the following equations is true considering Manning’s equation?
a) \(\frac{S_f}{S_0} = (\frac{y_n}{y})^{\frac{10}{3}}\)
b) \(\frac{S_f}{S_0} = (\frac{y}{y_n})^{\frac{10}{3}}\)
c) \(\frac{S_0}{S_f} = (\frac{y}{y_n})^{\frac{10}{3}}\)
d) \(\frac{S_0}{S_f} = (\frac{y_n}{y})^{\frac{10}{3}}\)
View Answer

Answer: a
Explanation:

6. The slope of the energy line of a wide rectangular channel is 4×10^-5 and the bed slope of the channel is 1 in 1200 using manning’s equation, calculate the depth in GVF if the uniform depth of flow is 1.5m.
a) 0.5m
b) 0.6m
c) 0.7m
d) 0.8m
View Answer

Answer: b
Explanation:

7. The value of slope of energy line of a wide rectangular channel is 3×10^-4 and the bed slope of the channel is 1 in 1500 using chezy’s equation, calculate the uniform flow depth if the depth during GVF is 2m.
a) 1.61m
b) 2.61m
c) 3.61m
d) 4.61m
View Answer

Answer: b
Explanation:

8. If y = 2m and velocity of flow is 2.5m⁄s, calculate the critical depth.
a) 0.36m
b) 1.36m
c) 2.36m
d) 3.36m
View Answer

Answer: b
Explanation:

9. Which of the following expressions is true?
a) \(\frac{dy}{dx} = S_0 \frac{((\frac{y}{y_n})^3-1)}{1-(\frac{y}{y_c})^3}\)
b) \(\frac{dy}{dx} = S_0 \frac{(1-(\frac{y}{y_n})^3)}{1-(\frac{y}{y_c})^3}\)
c) \(\frac{dy}{dx} = S_0 \frac{(1-(\frac{y_n}{y})^3)}{1-(\frac{y}{y_c})^3}\)
d) \(\frac{dy}{dx} = S_0 \frac{(\frac{y_n}{y})-1}{1-(\frac{y}{y_c})^3}\)
View Answer

Answer: a
Explanation:

10. Which of the following expressions is true?
a) \(\frac{dy}{dx} = S_0 \frac{((\frac{y}{y_n})^{\frac{10}{3}}-1)}{1-(\frac{y}{y_c})^3}\)
b) \(\frac{dy}{dx} = S_0 \frac{(1-(\frac{y}{y_n})^{\frac{10}{3}})}{1-(\frac{y}{y_c})^3}\)
c) \(\frac{dy}{dx} = S_0 \frac{(1-(\frac{y_n}{y})^{\frac{10}{3}})}{1-(\frac{y}{y_c})^3}\)
d) \(\frac{dy}{dx} = S_0 \frac{(\frac{y_n}{y})-1}{1-(\frac{y}{y_c})^3}\)
View Answer

Answer: a
Explanation:

11. If dy/dx=3×10^-4 m and the ratio of bed slope and slope of energy line is 0.7, calculate the value of slope of energy line if the uniform flow depth is 1.6m, critical depth is 1.2m.
a) 5.25×10^-4
b) 6.25×10^-4
c) 7.2510^-4
d) 8.25×10^-4
View Answer

Answer: d
Explanation:

12. If the ratio of GVF depth to normal depth and the ratio of critical depth to normal are equal to 0.5, calculate the rate of change of depth if the bed slope of the channel is 1 in 1300.
a) 5.96×^-4m
b) 6.96×^-4m
c) 7.96×^-4m
d) 8.96×^-4m
View Answer

Answer: c
Explanation:

13. Calculate the critical depth of a wide rectangular channel section if the normal depth and y_n are 3.2m and 2.5m respectively. Given: dy/dx=3×10^-4 m and S₀=1/2000.
a) 0.29m
b) 1.29m
c) 2.29m
d) 3.29m
View Answer

Answer: b
Explanation:

14. For a wide rectangular channel y>>B.
a) True
b) False
View Answer

15. If the velocity of flow through a wide rectangular channel is 2m⁄s and the rate of change of depth is 3×10^-5m, calculate the manning’s constant of the channel if the uniform flow depth is 1m and y_n=0.6m. Given: Critical depth = 0.5m.
a) 0.38×10^-3
b) 1.38×10^-3
c) 2.38×10^-3
d) 3.38×10^-3
View Answer

Answer: c
Explanation:

Sanfoundry Global Education & Learning Series – Fluid Mechanics.

To practice all areas of Fluid Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]