Fluid Mechanics Questions and Answers – Pressure Distribution in a Fluid – 2

This set of Fluid Mechanics Questions and Answers for Experienced people focuses on “Pressure Distribution in a Fluid – 2”.

1. Three beakers 1, 2 and 3 of different shapes are kept on a horizontal table and filled with water up to a height h. If the pressure at the base of the beakers are P₁, P₂ and P₃ respectively, which one of the following will be the relation connecting the three?

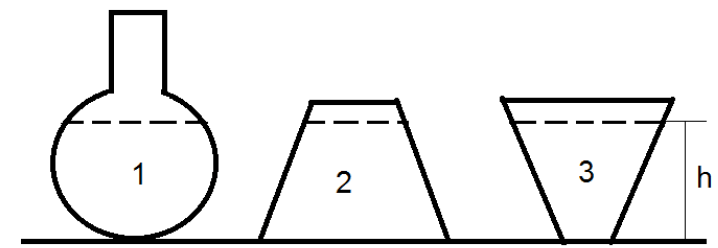
a) P₁ > P₂ > P₃
b) P₁ < P₂ < P₃
c) P₁ = P₂ = P₃
d) P₁ > P₂ < P₃
View Answer

2. A beaker is filled with a liquid of specific gravity S = 1:2 as shown. What will be the pressure difference (in kN/m²) between the two points A and B, 30 cm below and 10 cm to the right of point A?

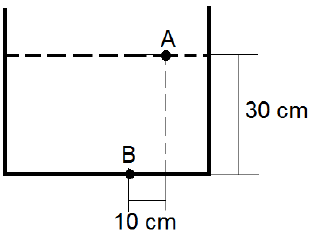
a) 2.5
b) 3.5
c) 4.5
d) 5.5
View Answer

3. The arm of a teapot is 10 cm long and inclined at an angle of 60^o to the vertical. The center of the arm base is 2 cm above the base of the beaker. Water is poured into the beaker such that half the arm is filled with it. What will be the pressure at the base of the beaker if the atmospheric pressure is 101.3 kPa?

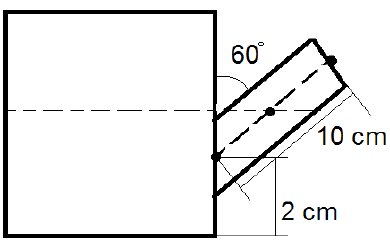
a) 101.3
b) 101.5
c) 101.7
d) 101.9
View Answer

4. A beaker of height 10 cm is half-filled with water (S_w = 1) and half-filled with oil (S_o = 1). At what distance (in cm) from the base will the pressure be half the pressure at the base of the beaker?

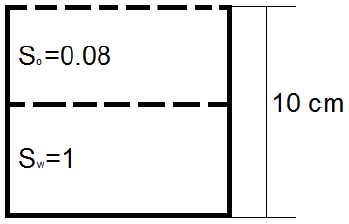
a) 4.375
b) 4.5
c) 5.5
d) 5.625
View Answer

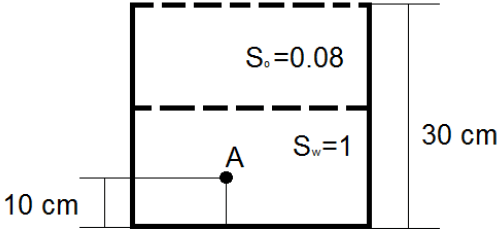
5. A beaker of height 30 cm is filled with water (S_w = 1) up to a height of 10 cm. Now oil (S_o = 0:9) is poured into the beaker till it is completely filled. At what distance (in cm) from the base will the pressure be one-third the pressure at the base of the beaker?

a) 27.33
b) 19.2
c) 10.8
d) 2.67
View Answer

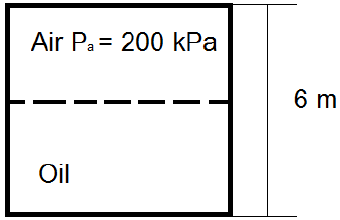
6. An oil tank of height 6 m is half-filled with oil and the air above it exerts a pressure of 200 kPa on the upper surface. The density of oil varies according to the given relation:

What will be the percentage error in the calculation of the pressure at the base of the tank if the density is taken to be a constant equal to 800?

a) 0.01
b) 0.05
c) 0.10
d) 0.15
View Answer

Answer: a
Explanation: The change of pressure with the vertical direction y is given by
dP/dy = – ρg
dP = -ρg dy
If P_a and P_b be the pressures at the top and bottom surfaces of the tank,

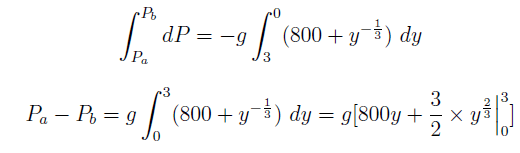
Thus, Pb = 223.5746kPa. If the density is assumed to be constant,
Pb = 200 + 800 * 9.81 * 3 * 10³ = 223.544 kPa. Hence, precentage error

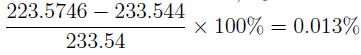
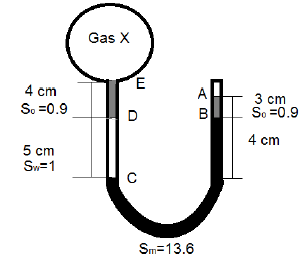
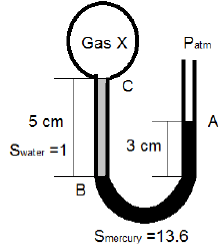
7. If a gas X be confined inside a bulb as shown, by what percent will the pressure of the gas be higher or lower than the atmospheric pressure? (Take the atmospheric pressure equal to 101.3 kPa)

a) 4:75% higher
b) 4:75% lower
c) 6:75% higher
d) 6:75% lower
View Answer

Answer: a
Explanation: P_a = P_atm = 101.3
P_b = P_a + 0.9 * 9.81 * 0.03 = 101.56
P_c = P_b + 13.6 * 9.81 * 0.04 = 106.9
P_d = P_c – 1 * 9.81 * 0.05 = 106.41
P_e = P_d – 0.9 * 9.81 * 0.04 = 106.1
P_X = P_e = 106.1
Since, P_X > P_atm, the percentage by which the pressure of the gas is higher than the atmospheric pressure will be

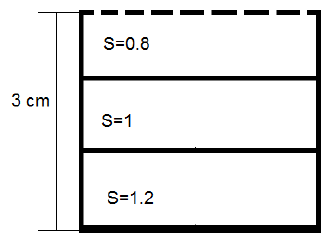
8. A tank of height 3 m is completely filled with water. Now two-third of the liquid is taken out and an equal amount of two other immiscible liquids of specific gravities 0.8 and 1.2 are poured into the tank. By what percent will the pressure at the base of the tank change?

a) 0%
b) 5%higher
c) 5%lower
d) 10%higher
View Answer

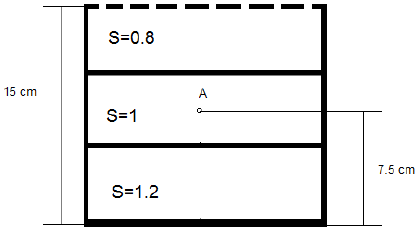
9. A beaker of height 15 cm is completely filled with water. Now two-third of the liquid is taken out and an equal amount of two other immiscible liquids of specific gravities 0.8 and 1.2 are poured into the tank. What will be the pressure (in kPa) at a point situated at a height, half the height of the beaker?

a) 588.6
b) 637.65
c) 735.75
d) 833.85
View Answer

10. A beaker of height h is completely filled with water. Now two-third of the liquid is replaced by another liquid. If the pressure at the base of the beaker doubled, what is the specific gravity of the liquid poured?
a) 0.5
b) 1
c) 2
d) 2.5
View Answer

Answer: d
Explanation: Pressure at the base initially = S_w * ^h⁄₃ * g; Pressure at the base after pouring the second liquid = S_w * ^h⁄₃ * g + S_l * ^2h⁄₃ * g, where S_w and S_l are the specific gravities of water and the second liquid.

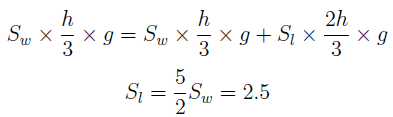
11. A beaker, partially filled with a liquid is rotated by an angle 30^o as shown. If the pressure at point B becomes 12 bar, what will be the height (in cm) of the beaker?

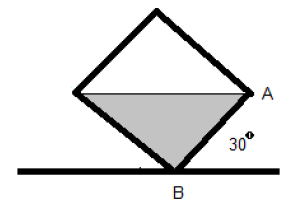
a) 23.5
b) 24.5
c) 26.5
d) 27.5
View Answer

12. A beaker of height 15 cm is partially filled with a liquid and is rotated by an angle θ as shown.
If the pressure at point B becomes 5 bar, what will be the value of θ?

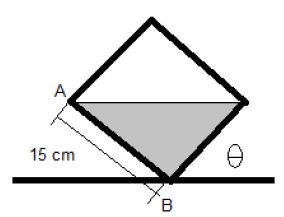
a) 30^o
b) 50^o
c) 60^o
d) 70^o
View Answer

13. A beaker of height 30 cm is partially filled with a liquid and is rotated by an angle θ as shown.
At this point, the pressure at point B is found to be 5 bar. By what angle should θ be increased such that the pressure at B gets halved?

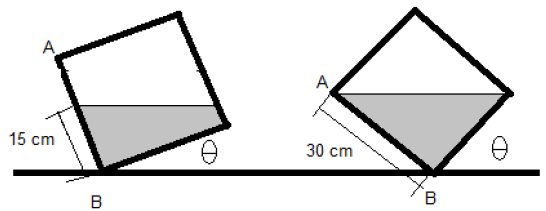
a) 12^o
b) 15^o
c) 17^o
d) 20^o
View Answer

14. A closed tank (each side of 5 m) is partially filled with fluid as shown. If the pressure of the air above the fluid is 2 bar, find the pressure at the bottom of the tank. Assume the density ρ of the fluid to vary according to the given relation:

a) 766
b) 776
c) 786
d) 796
View Answer

15. For what height of the mercury column will the pressure inside the gas be 40 cm Hg vacuum?

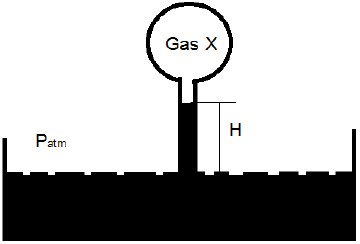
a) 36
b) 40
c) 76
d) 116
View Answer

Sanfoundry Global Education & Learning Series – Fluid Mechanics.

To practice all areas of Fluid Mechanics for Experienced people, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]