Fluid Mechanics Questions and Answers – Types of Fluids

This set of Fluid Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Types of Fluids”.

1. The relation between shear stress Z and velocity gradient 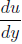of a fluid is given by 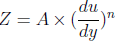where A and n are constants. If n = 1, what type of fluid will it be?
a) Newtonian fluid
b) Non-Newtonian fluid
c) Pseudoplastic
d) Bingham plastic
View Answer

Answer: a
Explanation: When n = 1, the relation reduces to Newton’s law of viscosity: z = A * 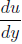, where A will represent the viscosity of the fluid. The fluid following this relation will be a Newtonian fluid.

2. The relation between shear stress Z and velocity gradient 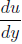of a fluid is given by 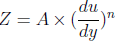where A and n are constants. If n > 1, what type of fluid will it be?
a) Newtonian fluid
b) Dilatant
c) Pseudoplastic
d) Bingham plastic
View Answer

Answer: b
Explanation: When n ≠ 1, the relation will be treated as Power law for Non-Newtonian fluids:
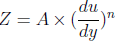. For n > 1, the rate of change of the shear stress increases with the increase in the value of velocity gradient. Such fluids are called Dilatants.

3. The relation between shear stress Z and velocity gradient 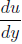of a fluid is given by 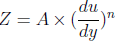where A and n are constants. If n < 1, what type of fluid will it be?
a) Newtonian fluid
b) Dilatant
c) Pseudoplastic
d) Bingham plastic
View Answer

Answer: c
Explanation: When n ≠ 1, the relation will be treated as Power law for Non-Newtonian fluids:
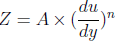. For n < 1, the rate of change of the shear stress decreases with the increase in the value of velocity gradient. Such fluids are called Pseudoplastics.

4. The relation between shear stress Z and velocity gradient 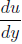of a fluid is given by 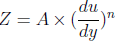+ B where A, n and B are constants. Which of the following conditions will hold for a Bingham plastic?
a) A = 0;B ≠ 0; n ≠ 1
b) A ≠ 0;B = 0; n ≠ 1
c) A = 0;B = 0; n = 1
d) A ≠ 0;B ≠ 0; n = 1
View Answer

5. The relation between shear stress Z and velocity gradient 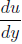of a fluid is given by 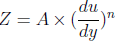+ B where A, n and B are constants. Which of the following conditions will hold for a Rheopectic?
a) A = 0;B ≠ 0; n > 1
b) A ≠ 0;B = 0; n < 1
c) A = 0;B = 0; n < 1
d) A ≠ 0;B ≠ 0; n > 1
View Answer

6. The relation between shear stress Z and velocity gradient 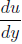of a fluid is given by 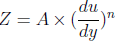+ B where A, n and B are constants. Which of the following conditions will hold for a Thixotropic fluid?
a) A = 0;B ≠ 0; n > 1
b) A ≠ 0;B = 0; n > 1
c) A = 0;B = 0; n < 1
d) A ≠ 0;B ≠ 0; n < 1
View Answer

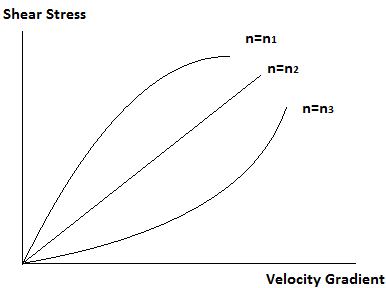
7. The graph shows relation between shear stress Z and velocity gradient 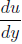of a fluid is given by 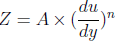where A and n are constants. The graphs are drawn for three values of n. Which one will be the correct relationship between n₁, n₂ and n₃?

a) n₁ > n₂ > n₃
b) n₁ < n₂ < n₃
c) n₁ > n₃ > n₂
d) n₁ < n₃ < n₂
View Answer

8. Which of the following is a shear-thinnning fluid?
a) Bingham plastic
b) Rheopectic
c) Dilatant
d) Pseudoplastic
View Answer

Answer: d
Explanation: Shear-thinning fluids are those which gets strained easily at high values of shear stresses. The relation between shear stress Z and velocity gradient 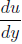of a shear-thinning fluid is given by 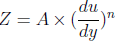, where A and n are constants and n < 1. This relation is followed by Pseudoplastics.

9. Which of the following is a shear-thickening fluid?
a) Bingham plastic
b) Thixotropic
c) Dilatant
d) Pseudoplastic
View Answer

Answer: c
Explanation: Shear-thickening fluids are those for which it gets harger to strain it at high values of shear stresses. The relation between shear stress Z and velocity gradient 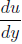of a shear-thickening fluid is given by 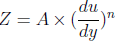where A and n are constants and n > 1. This relation is followed by Dilatants.

10. For what value of flow behaviour index, does the consistency index has a dimension independent of time?
a) 0
b) 1
c) 2
d) 3
View Answer

Answer: c
Explanation: The relation between shear stress Z and velocity gradient 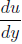of a fluid is given by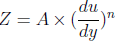
where A is the flow consistency index and n is the flow behaviour index.

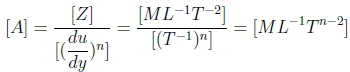
Thus [A] will be independent of time when n = 2.

11. What will be the dimension of the flow consistency index for a fluid with a flow behaviour index of 3?
a) [M L^-2 T].
b) [M L^-2 T^-1].
c) [M L^-1 T^-2].
d) [M L^-1 T].
View Answer

Answer: d
Explanation: The relation between shear stress Z and velocity gradient 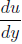of a fluid is given by 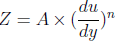where A is the flow consistency index and n is the flow behaviour index. Putting n = 3,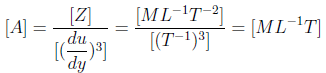

12. What will be the dimension of the flow consistency index for a fluid with a flow behaviour index of -1?
a) N/m² s²
b) N/m² s
c) N/ms
d) N/ms²
View Answer

Answer: b
Explanation: The relation between shear stress Z and velocity gradient 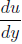of a fluid is given by 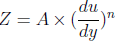where A is the flow consistency index and n is the flow behaviour index. If n = -1, A = Z * 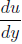Unit of Z is N/m² and 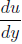is s^-1. Thus, the unit of A will be N/m² s.

Sanfoundry Global Education & Learning Series – Fluid Mechanics.

To practice all areas of Fluid Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]