This is a PLC Program to Implement Binary to Gray Code Conversion.
Problem Description
Implementing Binary to Gray Code conversion in PLC using Ladder Diagram programming language.
Problem Solution
- In Gray Code only one bit changes at a time.
- Write truth table showing the relation between Binary as input and Gray code as output.
- To obtain these equations, Karnaugh-Map method is again used.
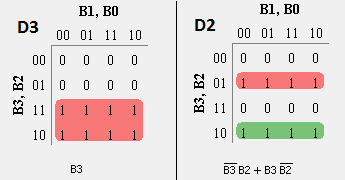
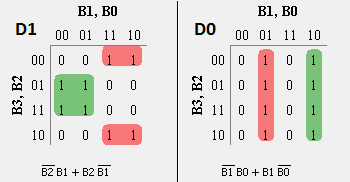
- For each Gray code output D3, D2, D1 and D0, write Karnaugh-Map.
- From the K-Map, obtaining a simplified expression for each Gray Code output in terms of Binary inputs.
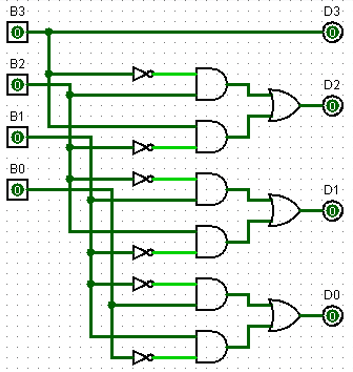
- Realize the code converter using the Logic Gates.
- By following actual process to convert Binary into Gray Code, Truth Table can be written as given below.
Truth Table relating Binary to BCD
Decimal Binary input Gray Code output B3 B2 B1 B0 D3 D2 D2 D0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 2 0 0 1 0 0 0 1 1 3 0 0 1 1 0 0 1 0 4 0 1 0 0 0 1 1 0 5 0 1 0 1 0 1 1 1 6 0 1 1 0 0 1 0 1 7 0 1 1 1 0 1 0 0 8 1 0 0 0 1 1 0 0 9 1 0 0 1 1 1 0 1 10 1 0 1 0 1 1 1 1 11 1 0 1 1 1 1 1 0 12 1 1 0 0 1 0 1 0 13 1 1 0 1 1 0 1 1 14 1 1 1 0 1 0 0 1 15 1 1 1 1 1 0 0 0
Boolean expression for each BCD bits can be written as
D3= m(8, 9, 10, 11, 12, 13, 14, 15) D2= m(4, 5, 6, 7, 8, 9, 10, 11) D1= m(2, 3, 4, 5, 10, 11, 12, 13) D0= m(1, 2, 5, 6, 9, 10, 13, 14)
advertisement
advertisement
Realizing code conversion using Logic Gates
PLC Program
Here is PLC program to Implement Binary to Gray Code Conversion, along with program explanation and run time test cases.
List of Inputs and Outputs
B3= I:1/0 (Input) B2= I:1/1 (Input) B1= I:1/2 (Input) B0= I:1/3 (Input) D3= O:2/0 (Output) D2= O:2/1 (Output) D1= O:2/2 (Output) D0= O:2/3 (Output)
Ladder Diagram to obtain Excess-3 code output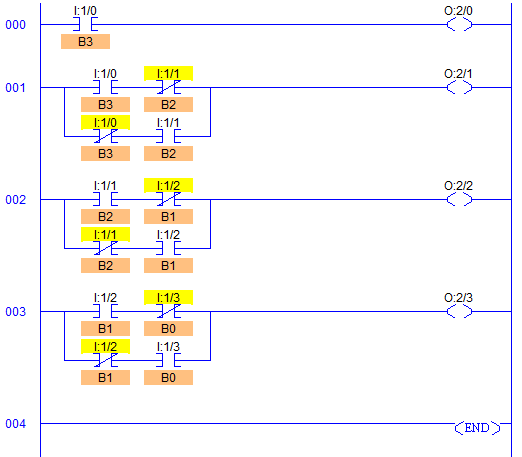
advertisement
Program Description
- RUNG000 to RUNG003 are to obtain D3 to D0 Gray Code output.
- Output D3 (O:2/0) is same as input B3 (I:1/0).
- Output D2 (O:2/1) is obtained by EX-ORing B3 (I:1/0) and B2 (I:1/1).
- Output D1 (O:2/2) is obtained by EX-ORing B3 (I:1/1) and B1 (I:1/2).
- Output D0 (O:2/3) is obtained by EX-ORing B2 (I:1/2) and B0 (I:1/3).
- This program description is also the actual process to convert any BCD number into Gray Code.
Runtime Test Cases
Decimal Binary input Gray Code output B3 B2 B1 B0 D3 D2 D2 D0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 2 0 0 1 0 0 0 1 1 3 0 0 1 1 0 0 1 0 4 0 1 0 0 0 1 1 0 5 0 1 0 1 0 1 1 1 6 0 1 1 0 0 1 0 1 7 0 1 1 1 0 1 0 0 8 1 0 0 0 1 1 0 0 9 1 0 0 1 1 1 0 1 10 1 0 1 0 1 1 1 1 11 1 0 1 1 1 1 1 0 12 1 1 0 0 1 0 1 0 13 1 1 0 1 1 0 1 1 14 1 1 1 0 1 0 0 1 15 1 1 1 1 1 0 0 0
Sanfoundry Global Education & Learning Series – PLC Algorithms.
To practice all PLC programs, here is complete set of 100+ PLC Problems and Solutions.
advertisement