This is a PLC Program to Implement Various Boolean Functions With Don’t Care Condition.
Problem Description
Implement given Boolean Function having don’t care conditions.
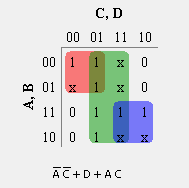
F(A,B,C,D)=∑m(0,1,5,9,13,14,15) + d(3,4,7,10,11)
Problem Solution
- Here in this equation inputs are A, B, C, and D and output is F (A, B, C, D) and d(3,4,7,10,11) denotes don’t care condition. To solve this problem, we must first minimize the equation by using Karnaugh-Map method which is given below.
- If don’t care condition exists, it means that output will not get affected by its state. Even if the state is true or false, output remains unchanged.
PLC Program
Here is PLC program to Implement Various Boolean Functions With Don’t Care Condition, along with program explanation and run time test cases.
List of Inputs and Outputs
advertisement
advertisement
A = I:1/0 (Input) B = I:1/1 (Input) C = I:1/2 (Input) D = I:1/3 (Input) F(A,B,C,D)= O:2/0 (Output)
Ladder diagram for the give expression
Program Description
- Output F(a,b,c,d)/O:2/0 here will go high in 3 conditions. As we can see from the ladder diagram and in the Boolean function which was solved using Karnaugh Map.
- There are 3 pairs of inputs connected in parallel to each other which represent OR function and connecting each of them pair of two inputs in AND function.
- Output goes high in following three conditions.
- Whenever D, that is when I:1/3 is high irrespective of other input states.
- Whenever A (I:1/0) and C (I:1/1) both are high irrespective of other input states.
- Whenever A (I:1/0) and C (I:1/1) both are low irrespective of other input states.
Runtime Test Cases
Inputs Output A B C D O:2/0 0 0 0 0 HIGH 0 0 0 1 HIGH 0 0 1 0 LOW 0 0 1 1 HIGH 0 1 0 0 LOW 0 1 0 1 HIGH 0 1 1 0 LOW 0 1 1 1 HIGH 1 0 0 0 LOW 1 0 0 1 HIGH 1 0 1 0 HIGH 1 0 1 1 HIGH 1 1 0 0 LOW 1 1 0 1 HIGH 1 1 1 0 HIGH 1 1 1 1 HIGH
Sanfoundry Global Education & Learning Series – PLC Algorithms.
To practice all PLC programs, here is complete set of 100+ PLC Problems and Solutions.
advertisement