This set of Engineering Physics Multiple Choice Questions & Answers (MCQs) focuses on “Retardation Plates”.
1. A plate which induces the desired amount of phase difference between two rays is known as ____________
a) Polaroid
b) Phasor plates
c) Retardation Plates
d) Quartz plates
View Answer
Explanation: Sometimes, it is required to induce a certain phase difference between E-ray and O-ray. For that, a plate with a specific thickness is chosen to induce that phase difference. This plate is known as the retardation plate as it retards the motion of one of the rays.
2. A quarter wave plate induces a phase shift of ___________
a) π/6
b) π/2
c) π/4
d) π/3
View Answer
Explanation: A quarter wave plate is a uniaxial, doubly refracting crystal plate. It induces a phase difference of π/2 between the O-ray and the E-ray.
3. Which phenomenon is used for inducing the phase shift in the retardation plates?
a) Reflection
b) Polaroid filters
c) Double Refraction
d) Polarimeter
View Answer
Explanation: The retardation plated uses double refraction for inducing the phase shift. They induce a phase shift between the O-ray and the E-ray.
4. If a ray is incident at 45° on a quarter-wave plate, the emergent light is ___________
a) Unpolarized
b) Linearly Polarized
c) Elliptically Polarized
d) Circularly Polarized
View Answer
Explanation: If the light is incident at an angle of 45° on the quarter-wave plate, then the emergent light would be circularly polarized. If the angle is not 45°, then it would be elliptically polarized.
5. A Half-wave plate induces a phase difference of ____________
a) π
b) π/4
c) π/2
d) π/3
View Answer
Explanation: A half wave plate is a uniaxial doubly refracting crystal that induces a phase difference of π or a path difference of λ/2 between the E-ray and the O-ray.
6. What should be the minimum thickness of a half-wave plate made of calcite for the light of wavelength 5500 Å? The principal refractive indices are 1.652 and 1.488.
a) 1.234 μm
b) 1.676 μm
c) 1.956 μm
d) 2.165 μm
View Answer
Explanation: As we know, t = \(\frac{\lambda}{2(\mu_E-\mu_0)}\)
Here, μe = 1.652 and μ0 = 1.488, λ = 5500 X 10-8 cm
Therefore, t = 5500/2 X 0.164 X 10-8 cm
= 1.676 μm.
7. If the thickness of a plate is 0.0032 cm, what shall be the phase retardation for a light of wavelength 5000 Å, given the principal refractive indices are 1.55 and 1.54?
a) 1.05π radians
b) 1.15π radians
c) 1.25π radians
d) 1.35π radians
View Answer
Explanation: Here, t = 0.0032 cm, μe = 1.55, μ0 = 1.54 and λ = 5000 X 10-8 cm
Phase retardation = \(\frac{2}{\pi\lambda}\)(μe – μ0)t
= 2π X 0.009 X 0.0032/5000 X 10-8
= 1.15π radians.
8.What should be the thickness of quarter-wave plate for a light of wavelength 5890 Å if μe = 1.553 and μ0 = 1.544?
a) 1.33 X 10-3 cm
b) 1.43 X 10-3 cm
c) 1.53 X 10-3 cm
d) 1.63 X 10-3 cm
View Answer
Explanation: t = \(\frac{\lambda}{2(\mu_E-\mu_0)}\)
λ = 5890 Å = 5890 X 10-8 cm, μe = 1.553 and μ0 = 1.544
Therefore, t = 5890a X 10-8/4 X 0.009
= 1.63 X 10-3 cm.
9. For what wavelength would a half wave plate behave as a half wave plate?
a) 2λ
b) λ/2
c) 3λ
d) Never
View Answer
Explanation: For a half-wave plate, t = \(\frac{\lambda}{2(\mu_E-\mu_0)}\)
Multiplying numerator and denominator with 2 we get, t = \(\frac{2\lambda}{4(\mu_E-\mu_0)}\)
As we can see, this resembles the expression for thickness of a quarter-wave plate, t = \(\frac{2\lambda}{4(\mu_E-\mu_0)}\). Thus, for λ’ = 2 λ, a half wave plate would behave as a quarter-wave plate.
10. How is the emergent beam polarized?
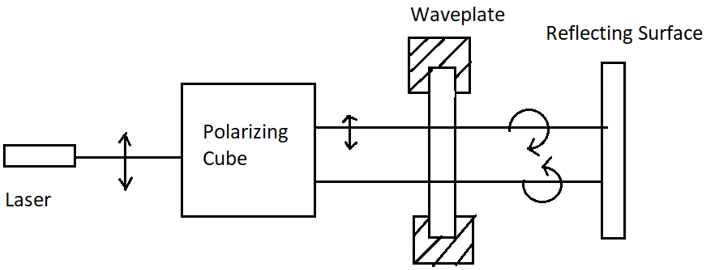
a) Linearly polarized
b) Circularly polarized
c) Elliptically polarized
d) Unpolarized
View Answer
Explanation: As we can see, a quarter wave plate is used in the given figure. The emergent beam is circularly polarized, as is clearly visible from the figure.
Sanfoundry Global Education & Learning Series – Engineering Physics.
To practice all areas of Engineering Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
