This set of Engineering Physics Multiple Choice Questions & Answers (MCQs) focuses on “Plane Diffraction Grating”.
1. If a is the width of the slits and b the distance between the slits, then a + b is called as _________
a) Opacities
b) Transparency
c) Grating Constant
d) Grating value
View Answer
Explanation: The sum of the width of the slits and the distance between the slits is called the grating constant of the grating. It can also be described as the separation between the corresponding point of two adjacent transparencies.
2. The CDs available in the market act as ____________
a) Diffraction grating
b) Reflection grating
c) Transmission grating
d) Do not act as a grating
View Answer
Explanation: The CDs have microscopic pits on its surface. It splits white light into its constituent colors and thus acts as a reflection grating. It is due to this that rainbow colors can be seen on CD surface.
3. Which of the following is the correct expression for the ratio of the intensity of principal maxima to the intensity of secondary maxima?
a) 1 + (N2-1) sin2β
b) 1/1 + (N2-1) sin2β
c) (N2-1) sin2β
d) 1/(N2-1) sin2β
View Answer
Explanation: The expression 1 + (N2-1) sin2β is the relation for the ratio of the intensity of principal maxima to that of the secondary maxima. It shows that the intensity of secondary maximas are inversely proportional to N.
4. If there are N number of slits in a grating spectra, then there will be how many secondary maximas?
a) N
b) N – 1
c) N – 2
d) 2N
View Answer
Explanation: Between any two consecutive principal maxima, there is a set of smaller secondary maxima and minima. Thus, there would be N – 1 secondary minimas and N – 2 secondary maximas.
5. If (a + b) < nλ, then nth order spectrum will be absent.
a) True
b) False
View Answer
Explanation: We know that according to the grating rule,
(a + b) sinθ = nλ
Now, if (a + b) < nλ then sinθ > 1 which is not possible. Hence, in that case, the nth order spectrum will be absent.
6. The expression for the maximum number of orders in a grating spectrum is given by ____________
a) λ/ (a + b)
b) a/λ
c) b/λ
d) (a + b)/ λ
View Answer
Explanation: We know that, (a + b) sinθ = nλ
Therefore, n = (a + b) sinθ/λ
Now, as the maximum value for sinθ is 1. Hence,
nmax = (a + b) /λ.
7. What is the relation between the dispersive power, D, of a grating and the order, n, of a spectrum?
a) D ∝ n
b) D ∝ N2
c) D ∝ 1/n
d) D ∝ 1/N2
View Answer
Explanation: The dispersive power of a grating is given by:
∂θ/∂λ = n/ (a + b) cosθ
Thus, as we can see D ∝ n. Hence, higher the order, higher is the dispersive power.
8. A beam of monochromatic light is incident on a plane transmission grating having 5000 lines/cm and the second order spectral line is found to be diffracted at 30°. The wavelength of the light is _______
a) 4000 Å
b) 5000 Å
c) 6000 Å
d) 7000 Å
View Answer
Explanation: Here, N = 5000, a + b = 1/5000 cm
Now using, (a + b) sinθ = nλ for second order spectrum we get,
λ = sin30°/ 2 X 5000 cm
λ = 5000 Å.
9. What is the highest order spectrum which may be seen with a monochromatic light of wavelength 5000 Å by means of a diffraction grating with 5000 lines/cm?
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: Here, N = 5000. Therefore, a + b = 1/5000 cm
Now, as we know, Nmax = a + b/λ
= 1/5000 X 5000 X 10-8
= 4.
10. A grating has 16000 per inch over a length of 5 inches. What will be the smallest wavelength difference for a light of wavelength 6000 Å?
a) 0.01 Å
b) 0.02 Å
c) 0.03 Å
d) 0.04 Å
View Answer
Explanation: N = 16000 X 5 = 80000, n = 2
Wavelength = 6 X 10-5 cm
Resolving power = nN = 2 X 80000 = 160000
Smallest wavelength difference = λ/nN
= 0.0375 Å.
11. What is shown by the following curve?
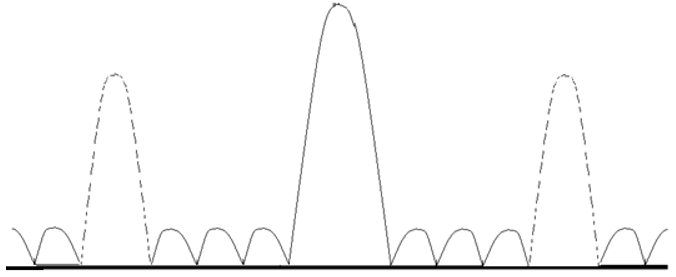
a) Resultant Amplitude Curve
b) Resultant Interference Pattern
c) Resultant Intensity Curve
d) Resultant Diffraction Pattern
View Answer
Explanation: The following graph shows the resultant intensity variation of the pattern observed by a plane transmission grating. As we can see, between two principal maximas, there are secondary maximas and minimas.
12. For a plane transmission grating with 5000 lines/cm what are the the absent order spectra if the width of the opacity is twice that of the frequency?
a) 1st, 3rd, 5th, …
b) 2nd, 4th, 6th, …
c) 3rd, 6th, 9th, …
d) 4th, 8th, 12th,…
View Answer
Explanation: Now, for the order n to be missing
\(\frac{a+b}{a}=\frac{n}{M}\)
n/m = 1 + b/a
n/m = 3
n = 3m
Hence, the missing order spectra are 3rd, 6th, 9th, …
13. A diffraction grating has 4000 lines/cm. The dispersive power of the grating in the third order spectrum in the wavelength region of 5000 Å is _____________
a) 5000
b) 10000
c) 15000
d) 20000
View Answer
Explanation: We know; the dispersive power of a grating is given by:
\(\frac{\partial \theta}{\partial \lambda}\) = n/(a + b) cosθ
Now, here n = 3 and a + b = 1/5000 cm
Here, sinθ = nλ/(a + b) = 0.6
cosθ = 0.8
Now, \(\frac{\partial \theta}{\partial \lambda}\) = 3 X 4000/0.8
= 15000.
Sanfoundry Global Education & Learning Series – Engineering Physics.
To practice all areas of Engineering Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
