This set of MATLAB Multiple Choice Questions & Answers (MCQs) focuses on “Impulse Response – 2”.
1. The impulse response does not take account of the transient response of the system.
a) True
b) False
View Answer
Explanation: Since the output of a system depends on int’s initial conditions, the laplace transform of the output would depend on the transient conditions. Hence, the impulse response of the system does take account of the transient response of the system.
2. The impulse response of a parabola _________
a) will have 3 poles in the s-plane
b) will have 2 poles in the s-plane
c) will have 4 poles in the s-plane
d) will have no poles in the s-plane
View Answer
Explanation: The transfer function of a system, whose impulse response is a parabola, will have three roots which will satisfy the characteristic equation. Hence, only option will have 3 poles in the s-plane is correct.
3. The impulse response of a sinusoid ________
a) will have 2 poles in the s-plane
b) will have 3 poles in the s-plane
c) will have 1 pole frequency in the s-plane
d) will have only 1 conjugate pole in the s-plane
View Answer
Explanation: The transfer function of the system, whose impulse response is a sinusoid, will have 2 roots which satisfy the characteristic equation. Hence, there will be two poles which are complex conjugate to each other.
4. The step response of the impulse response of a ramp function will be ________
a) a parabolic function
b) an exponential function
c) a sinusoidal function
d) a sinc function
View Answer
Explanation: The step response of a system can be thought in the Laplace domain as multiplication with 1/s. Now, the impulse response of ramp function is the ramp function itself while the step response of ramp function results in a parabola.
5. In MATLAB, the impulse response of the step response of a system is ___ to the step response of the impulse response of the system.
a) Equal
b) Not Equal
c) Greater
d) Lesser
View Answer
Explanation: The distributive property of convolution suggests that the A*(B*C)=(A*B)*C. Thus only option Equal is correct.
6. The impulse response of the transfer function 1 is ________
a) an impulse function
b) a step function
c) a pulse function
d) cannot be determined
View Answer
Explanation: The laplace transform of only the impulse function is 1. Hence, the inverse laplace transform.
7. What is the output of the following code?
>>p=ilaplace(1); >>laplace(p)
a) 1
b) Impulse function
c) Error
d) Cannot be determined
View Answer
Explanation: The ilaplace command doesn’t take double as an input. This would lead to an error and the correct option is Error.
8. What is the output of the following code?
>>p=ilaplace(s/s); >>laplace(p)
a) dirac(1,t)
b) dirac[1,t]
c) dirac{1,t}
d) Cannot be determined
View Answer
Explanation: The ilaplace command observes that the input is actually 1. The inverse laplace transform of 1 is the impulse function which is represented as dirac(1,t) in MATLAB.
9. What is the output of the following code?
>>t=(0:17); >>o=dirac(t)==Inf; >>q=o*1; >>conv(q,t)
a) t followed with 17 zeros
b) t followed with 18 zeros
c) 1
d) Error
View Answer
Explanation: In the above code, we’ve actually performed the impulse response of discrete system defined by a ramp function for [0,17]. Now, the output of the code is shown below which shows that the impulse function gets shifted for the time t and the total result of the convolution will be the entire value. Notice that the length of the convolution is 2N-1=35.
Output:
10. The impulse response is the result of the transfer function of the system.
a) True
b) False
View Answer
Explanation: The impulse response is truly due to the impulse input given to a system. If we would’ve changed the input, the output would’ve been a different and the resulting expression in laplace domain will not be called the transfer function.
11. What is the output of the following code?
>>t=(0:17); >> p=dirac(0)==Inf; >> q=p*1; >> conv(q,t)
a) An impulse response of step for a time from 0:16
b) An impulse response of unit ramp function for a time from 0:17
c) An impulse response of ramp function for a time from 0:18
d) Error in 3rd line
View Answer
Explanation: The function p exists for only t=0 and q has only 1 element in it which is 1. So, truly, we’ve derived the convolution of a system which results in a ramp function whose slope is 1 and is ranging from 0 to 17 units in time since t is defined as such.
Output:
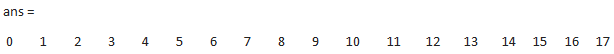
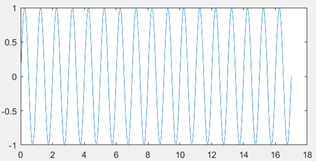
12. What is the output of the following code?
>> p=dirac(0)==Inf; >> t=(0:.001:17); >> q=p*1; >> conv(q,sin(2*pi*t)); >> plot(t,ans)
a) A sinusoid of a frequency 1Hz
b) A sinusoid of a frequency of 17 Hz
c) A sinusoid of a frequency of .001 Hz
d) Error
View Answer
Explanation: We’re only computing the impulse response of a system which behaves as a sinusoid on the input. The frequency of the system is 1 Hz as seen from the description. The output, shown below, contains 17 cycles.
13. What is the slope of the ramp function?
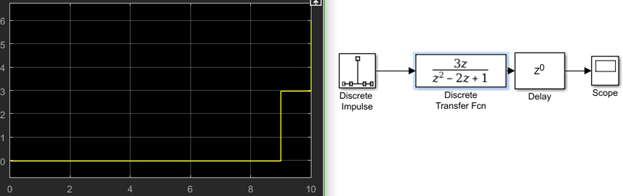
a) 3
b) 2
c) 1
d) 6
View Answer
Explanation: The transfer function window shows that it holds the z-transform of a ramp function. But we observe from the graph that the output changes with a step of 3. Hence, the slope of the ramp function is 3 since we are plotting the impulse response of the system.
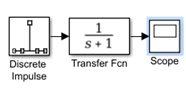
14. What is the output at the scope?
a) 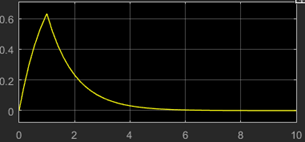
b) 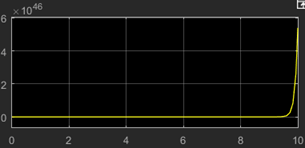
c) 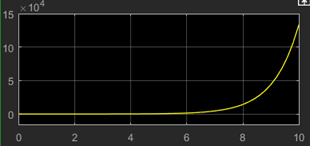
d) 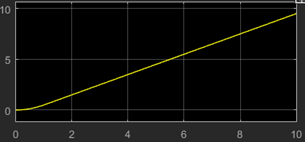
View Answer
Explanation: The transfer function represents an exponentially decaying step function.Graph shows a ramp function which doesn’t have a transfer function depicted in the above figure.
15. What does the following relate to?
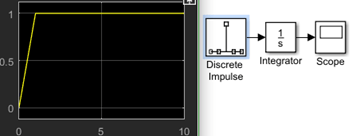
a) Step response implies integrating the transfer function
b) Impulse response shows the delay in the above block diagram
c) Nothing is observed
d) The integration of impulse is a ramp function
View Answer
Explanation: The above block diagram depicts that the impulse response of the integrator is a step function. This means that an integrator can be viewed as performing convolution of a step function and the input. Now if we imagine a system which has the same transfer function as the lapalce transform of the previous input, and we give a step input to it- it will perform convolution of the step function an the system transfer function. Thus we find that the result, due to associative property of convolution, is same and we can represent that the step response of system truly implies integrating the transfer function of the system in the output.
Sanfoundry Global Education & Learning Series – MATLAB.
To practice all areas of MATLAB, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]