This set of Signals & Systems Multiple Choice Questions & Answers (MCQs) focuses on “Convolution : Impulse Response Representation for LTI Systems – 1”.
1. Impulse response is the output of ______ system due to impulse input applied at time=0?
a) Linear
b) Time varying
c) Time invariant
d) Linear and time invariant
View Answer
Explanation: Impulse response is the output of LTI system due to impulse input applied at time = 0 or n=0. Behaviour of an LTI system is characterised by the impulse response.
2. Which of the following is correct regarding to impulse signal?
a) x[n]δ[n] = x[0]δ[n]
b) x[n]δ[n] = δ[n]
c) x[n]δ[n] = x[n]
d) x[n]δ[n] = x[0]
View Answer
Explanation: When the input x[n] is multiplied with an impulse signal, the result will be impulse signal with magnitude of x[n] at that time.
3. Weighted superposition of time-shifted impulse responses is termed as _______ for discrete-time signals.
a) Convolution integral
b) Convolution multiple
c) Convolution sum
d) Convolution
View Answer
Explanation: Weighted superposition of time-shifted impulse responses is called convolution sum for discrete-time signals and convolution integral for continuous-time signals.
4. Which of the following is a correct expression for Impulse response?
a) x[n] = \(∑_{k=-∞}^∞\) x[k]δ[n-k]
b) x[n] = \(∑_{k=-∞}^∞\) x[k]δ[n]
c) x[n] = \(∑_{k=-∞}^∞\) x[k]δ[k]
d) x[n] = \(∑_{k=-∞}^∞\) x[k]δ[nk]
View Answer
Explanation: X [n] is represented as the weighted sum of time shifted impulses and concisely written as x[n] = ∑∞k=-∞ x[k]δ[n-k]..
5. Determine the output of a LTI system,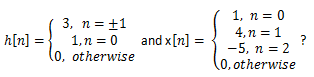 
a)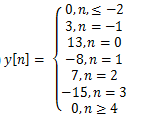 
b)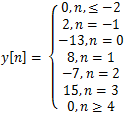 
c)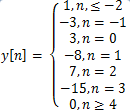 
d)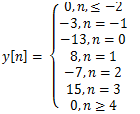 
View Answer
Explanation: X [n] is written as x[n]=δ[n]+4δ[n-1]-5δ[n-2] and y[n]=h[n]+4h[n-1]-5h[n-2]. By substituting the values for n = ….-2,-1, 0, 1, 2…. And corresponding h [n] we get y [n].
6. Determine the output of LTI system to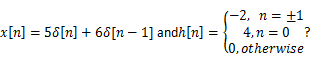 
a)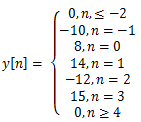 
b)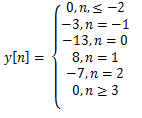 
c)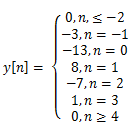 
d)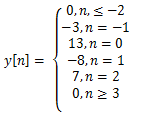 
View Answer
Explanation: x[n]=5δ[n]+6δ[n-1] andy[n]=5h[n]+6h[n-1]. By substituting the values for n = ….-2,-1, 0, 1, 2…. And corresponding h[n] we get the output sequence y[n].
7. Find the convolution sum of sequences x1[n] = (1, 2, 3) and x2[n] = (2, 1, 4).
a) {2, 5, 12, 11, 12}
b) {2, 12, 5, 11, 12}
c) {2, 11, 5, 12, 12}
d) {-2, 5,-12, 11, 12}
View Answer
Explanation: x1[n] = δ(n)+2δ(n-1)+3δ(n-2) and x2[n] = 2δ(n)+δ(n-1)+4δ(n-2)
Y[n] = x1[n]*x2[n] by performing convolution operation on x1[n] and x2[n] we get the sequence as {2, 5, 12, 11, 12}.
8. Find the convolution sum of sequence x1[n] = {1, 2, 3} and ![Find the convolution sum of sequence x1[n] = {1, 2, 3}](https://www.sanfoundry.com/wp-content/uploads/2018/08/signals-systems-questions-answers-convolution-impulse-response-representation-lti-systems-1-q8a.png){kind=small}
a)
{1, 4, 10, 16, 17, 12}
↑
b)
{1, 4, 10, 16, 17, 12}
↑
c)
{1, 4, 10, 16, 17, 12}
↑
d)
{1, 4, 0, 16, 17, 2}
↑
View AnswerExplanation: x1[n] and x2[n] can be written as x1[n] = δ(n)+2δ(n-1)+3δ(n-2) and
x2[n] = δ(N+2) + 2 2δ(n+1) + 3δ(n) + 4δ(n-1) and convolving x1[n], x2[n] we get
Y [n] =
{1, 4, 10, 16, 17, 12}
↑
9. Determine the output of LTI with input x[n] =2δ(n)-δ(n-1) and h[n] given as below.
![Find the output of LTI with input x[n] =2δ(n)-δ(n-1) & h[n] given as below](https://www.sanfoundry.com/wp-content/uploads/2018/08/signals-systems-questions-answers-convolution-impulse-response-representation-lti-systems-1-q9.png)
a) {2, 5, 1,-4, 3,-1}
b)
{2, 5, 1,-4, 3,-1}
↑
c)
{-2, 5, 1, 4, 3, 1}
↑
d)
{2,-5, 1, 4,-3,-1}
↑
View AnswerExplanation: The h[n] can be written as
{1, 3, 2,-1, 1}.
↑
By convolving x[n] with the given h[n] we get the following sequence as result
Y [n] = {2, 5, 1, -4, 3, -1}.
↑
10. Consider h [n] as in figure 1 and x[n] = u[n] – u [n-3], determine the output y [n] of the LTI system?
a)
{1, 4, 6, 4, 2, 0, 1}
↑
b)
{1, 4, 6,-4, 2, 0, 2, 1}
↑
c)
{1, 4, 6,-4, 2, 0,-1}
↑
d) {-1, 4, 6, 4, 2, 0,-1}
View Answer
Explanation: The h[n] can be written as
{1, 3, 2,-1, 1}.
↑
By convolving x [n] with the given h [n] we get the output
y [n] = {1,4,6,4,2,0,1}.
↑
Sanfoundry Global Education & Learning Series – Signals & Systems.
To practice all areas of Signals & Systems, here is complete set of 1000+ Multiple Choice Questions and Answers.
