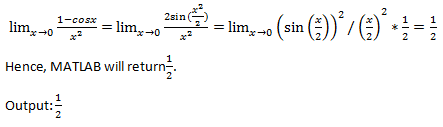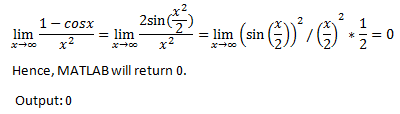This set of MATLAB Multiple Choice Questions & Answers (MCQs) focuses on “Limits – 1”.
1. Can we check the continuity of a function in MATLAB?
a) Yes
b) No
c) Sometimes
d) Rarely
View Answer
Explanation: With the help of the limit function, we can check the left-hand limit and right-hand limit for a function approaching a limiting value. We can also check the value of the function at the limiting value. Thus, we can check the continuity of a function at the limiting value.
2. What is the output of the following code?
limit(x^2,x,1,’left’)
a) 1
b) 0
c) x should be declared symbolic
d) Cannot be determined
View Answer
Explanation: We haven’t initialized x as a symbolic variable. But the command limit() requires an argument which will initialize the function variables as symbolic. We have given x as an input to our command but we haven’t declared it as a symbolic variable. Hence MATLAB will show an error. If we had written syms x, the answer would have been 1.
3. What is the error in the following code?
limit(x^2,y,1,'left')
a) The function
b) The symbolic argument
c) Left should’ve been without
d) No error
View Answer
Explanation: Our function does not have the character y. Hence, when we introduce y as an argument, MATLAB will show an error. If we had written limit(x^2,x,1,’left’)- the answer would’ve been 1.
4. How can we check whether the limn→3+ n-1 exists?
a) limit(n-1,n,3)
b) syms n;limit(n-1,n,3,’right’)
c) syms n;limit(n-1,3,’right’)
d) syms n;limit(n-1,3,n,’right’)
View Answer
Explanation: We have to give our symbolic argument before our limit command. Hence, syms n;limit(n-1,n,3,’right’) has the right order, and not syms n;limit(n-1,3,n,’right’). syms n;limit(n-1,n,3,’right’) is not same as limit(n-1,n,3) since there we are calculating the value of the function at the limiting value, 3, but we need to find it at the right-hand side of the limiting value- plus, limit(n-1,n,3) does not declare n as symbolic- this will give an error. syms n;limit(n-1,3,’right’) will give an error since the symbolic argument is not provided into the command.
5. What is the output of the following code?
syms n;limit(n-1,n,Inf,’right’)
a) Inf
b) Nan
c) 0
d) Error
View Answer
Explanation: We cannot approach the limiting value Infinity from the right-hand side. So, MATLAB will return an error while trying to run the code. The answer would have been Inf if the limiting value was approached from the left hand side.
6. What is the output of the following code?
syms n;limit(n-1,n,nan,'left')
a) 0
b) Inf
c) Nan
d) Error
View Answer
Explanation: Nan in MATLAB signifies Not a number. If we give Nan as a limiting value argument to our limit command, it will not give an error. Instead, it will return Nan as the result. The result is not helpful at all. The result would have been 0 if the limiting value was 1.
Output: Nan
7. What is the output of the following code?
syms x;limit(((1-cos(x))/(x^2)),x,0)
a) 0
b) 1⁄2
c) Error
d) Infinite
View Answer
8. What is the output of the following code?
syms x;limit(((1-cos(x))/(x^2)),x,Inf)
a) Inf
b) 0
c) Nan
d) Error
View Answer
9. What is the output of the following code?
syms x;limit((((Inf*x)-cos(x))/(x^2)),x,0)
a) limit(Inf/x, x, 0)
b) Inf
c) Nan
d) Error
View Answer
Explanation: We observe that the numerator is Infinite and the denominator tends to 0. Hence the function is of the form ∞/0. This is an inbuilt form in MATLAB and MATLAB returns option a whenever it faces such a function. The result is of symbolic class.
Output: limit(Inf/x, x, 0)
10. What is the output of the following code?
limit(0/0, x, 0)
a) Nan
b) Inf
c) 0
d) Error
View Answer
Explanation: The 0/0 is an indeterminate form. MATLAB will return a Nan if it comes across an indeterminate form.
11. If a function is differentiable, the function is continuous.
a) True
b) False
View Answer
Explanation: If a function is differentiable, it should be continuous in the domain where it is differentiable. This is because if the function is not continuous, within a range, it cannot be differentiated within that range.
12. What is the code to solve limx→1(logx)logx?
a) syms x;limit(‘log(x)^(log(x))’,x,1)
b) limit(‘log(x)^(log(x))’,x,1)
c) syms x;limit(log(x)^(log(x)),x,1)
d) Cannot be solved
View Answer
Explanation: We should not give the function as an input to the limit command as a string. It will generate a warning but gives an output. We have to declare our variables as symbolic before placing our function as an argument to the limit command.
13. What is the output of the following code?
sym x;limit(log(x)^(log(x)),x,1)
a) Error
b) 1
c) 0
d) Cannot be defined
View Answer
Explanation: When we declare a symbolic character, we use syms. If we use sym, the symbolic character is assigned to the variable ans. So, we haven’t defined x as symbolic; we have defined ans as a symbolic character which points to the character x. So, MATLAB will give an error because it cannot find x as a symbolic character. If we change the code to sym x;limit(log(ans)^(log(ans)),x,1); the answer would be 1.
14. What is the output in the following case?
syms x; limit(sin(x)/x)
a) 0
b) 1
c) Error
d) garbage value
View Answer
Explanation: If we do not give a limiting value to our limit command, the default limiting value will be taken as 0. Hence, the output of the following code will be 1.
15. What will be the output of the following code?
sym x;limit(‘log(x)^(log(x))’,1,’right’)
a) Error
b) 0
c) 1
d) Nan
View Answer
Explanation: While calculating left-hand limits or right-hand limits, we need to give our symbolic input as an argument to our limit() command. This is an inbuilt command so we will have to follow the syntactical constraints while doing such problems.
Sanfoundry Global Education & Learning Series – MATLAB.
To practice all areas of MATLAB, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]