This set of Spaceflight Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Ballistic Missiles Trajectories – Launching Errors Effect”.
1. In how many categories are the launching errors classified into?
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: There’s error produced when there’s variation in the speed, launch direction, position of the ballistic missile. They are classified into two errors-down-range errors, out-of-plane errors.
2. Which of these errors cause missile to deviate from the target in a different plane?
a) Incorrect Speed at Burnout
b) Effect of Down-Range Displacement of the Burnout Point
c) Effect of a Lateral Displacement of the Burnout Point
d) Incorrect Speed at Burnout
View Answer
Explanation: Only the effect of lateral displacement at the burnout among the options results in the missile to hit to right or left of the target i.e., it is a out-of-plane error. Rest of them are down-rage errors and the error in the intended plane causes either a long or a short hit.
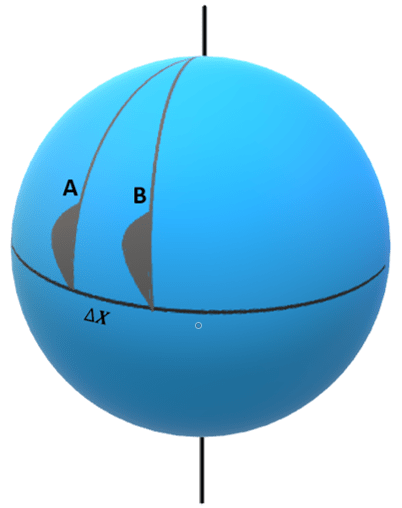
3. What is the formula used to compute the cross-range error due to the effect of the lateral displacement of the burnout point? (Where ΔX is the displacement of thrust cutoff point)
a) ΔC ≅ ΔX cosψ
b) ΔC ≅ ΔX sinψ
c) ΔC ≅ ΔX tanψ
d) ΔC ≅ ΔX secψ
View Answer
Explanation: If the thrust cutoff point is displaced by an amount ΔX, perpendicular to the intended plane of the trajectory and all other conditions are nominal, the cross-range error, ΔC at impact can be determined from spherical trigonometry.
Both ΔX and ΔC may be thought of as angles.
On applying the law of cosines for spherical to triangle OAB
cosΔC = sin2 ψ + cos2 ψ cosΔX
Using small angle approximation, we get:
ΔC ≅ ΔX cosψ
4. For a free-flight range of 90 degrees, the cross range error ΔC produced due to the lateral displacement of burnout point is zero.
a) True
b) False
View Answer
Explanation: Cross-range error is zero for a free-flight range of 90 degree. As the formula to compute the error produced due to the lateral displacement of burnout point is:
ΔC ≅ ΔX cosψ
The value of cos 90 is 0.
5. What is the formula used to compute the cross-range error due to incorrect launch azimuth? (Where Δβ is the is the displacement of launch azimuth from original azimuth launch)

a) ΔC ≅ Δβ tanψ
b) ΔC ≅ Δβ secψ
c) ΔC ≅ Δβ sinψ
d) ΔC ≅ Δβ cosψ
View Answer
Explanation: If the actual launch azimuth differs from the intended launch azimuth by an amount, Δβ, a cross-range error, ΔC will result. Since all launch conditions are assumed to be nominal except launch azimuth, the free-flight range of both the actual and the intended trajectories is ψ.
On applying the law of cosines for spherical to triangle:
cosΔC = cos2 ψ + sin2 ψ cosΔβ
Using small angle approximation, we get:
ΔC ≅ Δβ sinψ
6. For a free- flight range of 90 degrees, the cross range error ΔC produced due to the incorrect launch azimuth is zero?
a) True
b) False
View Answer
Explanation: Cross-range error is maximum for a free-flight range of 90 degree and goes to zero for 180 degree. The formula to compute the error is:
ΔC ≅ Δβ sinψ
The value of sin 90 is 1 and sin 180 is 0.
7. If the error in down-range position at thrust cutoff is 5nm, then what will be the error at the impact?
a) 0 nm
b) 5 nm
c) 10 nm
d) 20 nm
View Answer
Explanation: An error in down-range position at thrust cutoff produces an equal error at impact. If the actual burnout point is 5 nm farther down-range than was intended, the missile will overshoot the target by exactly 5 nm.
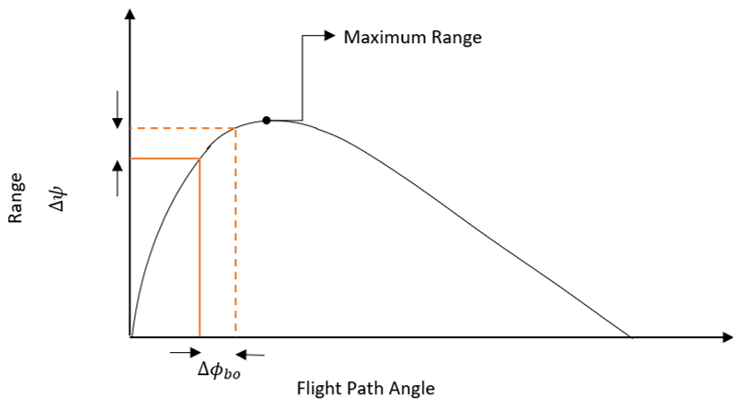
8. What is the formula used to compute the down-range error due to error in burnout flight-path angle? (Where ΔΦbo is the is the error in burnout flight-path angle)
a) Δψ ≅ \(\frac{\partial \phi_{bo}}{\partial \psi}\) ΔΦbo
b) Δψ ≅ \(\frac{\partial \psi}{\partial \phi_{bo}}^2\) ΔΦbo
c) Δψ ≅ \(\frac{\partial \psi}{\partial \phi_{bo}}\) ΔΦbo
d) Δψ ≅ \(\frac{\partial \phi_{bo}}{\partial \psi}^2\) ΔΦbo
View Answer
Explanation: The intended flight-path angle and intended range are shown by a solid line in the figure given below. If the actual Φbo differs from the intended value by an amount ΔΦbo, the actual range will be different by an amount Δψ. This Δψ represents a down-range error causing the missile to undershoot or overshoot the target.
9. If the burnout occurs at a higher height than intended, then where does the missile fall?
a) Missile overshoots the target
b) Missile falls short of the target
c) Missile falls at the exact point of the target
d) Missile falls to the right of the target
View Answer
Explanation: If the burnout occurs higher than intended, the missile overshoots and if burnout occurs too low, the missile falls short of the target in every case. The formula to compute the down- rage error due to incorrect burnout height is:
Δψ ≅ \(\frac{\partial \psi}{\partial r_{bo}}\) Δrbo
Where, rbo is the burnout radius.
10. If the missile’s burnout peed is slow, what happens to the magnitude of error while It lands on the target?
a) Missile overshoots the target
b) Missile falls short of the target
c) Missile falls at the left of the target
d) Missile falls to the right of the target
View Answer
Explanation: Speed at burnout affects range as causing down-range error. If the missile is too fast at the burnout, it overshoots and if it is too slow, the missile falls short. The magnitude of the error is:
Δψ ≅ \(\frac{\partial \psi}{\partial v_{bo}}\) Δvbo
Where, vbo is the burnout velocity.
Sanfoundry Global Education & Learning Series – Spaceflight Mechanics.
To practice all areas of Spaceflight Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
