This set of Orbital Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Non-Hohmann Transfer”.
1. What is the key feature of the Non-Hohmann transfer which is not present in a Hohmann transfer?
a) Common plane
b) Transfer between elliptical orbit
c) Transfer is tangent to both the orbit
d) Transfer shares the apse line to both the orbits
View Answer
Explanation: In both Hohmann and Non-Hohmann transfers, there’s a transfer between the two co-axial elliptical orbits. The main difference is that in Hohmann transfer, the transfer trajectory is tangent to both the initial and final orbits, whereas in Non-Hohmann that is not true. In the later case, both the orbits share a common apse line.
2. There is a higher change in specific energy when the satellite’s flight path angle is 90 degrees.
a) True
b) False
View Answer
Explanation: The change in specific energy is given by:
Δε = vΔv cosΦ + \(\frac{1}{2}\) Δv2
According to this, for a given Δv the change in specific energy is larger the faster the spacecraft is moving except when flight path angle becomes 90 degrees because then cos90 = 0.
3. If a satellite in orbit 1 produces a delta-v maneuver at point A and moves the second orbit, what is the flight path angle at point A (Given- True anomaly θA = 160 degrees)?
a) 9.171 degrees
b) 12.768 degrees
c) 14.368 degrees
d) 11.187 degrees
View Answer
Explanation: Given, rB = 15,000 km, rC = 8,000 km, θA = 160 degrees
We first calculate the eccentricity of the orbit:
e = \(\frac{r_B – r_C}{r_B + r_C} = \frac{15,000 – 8,000}{15,000 + 8,000}\) = 0.3043
Next, we compute the angular momentum using the formula:
h = \(\sqrt{2\mu} \sqrt{\frac{r_B r_C}{r_B + r_C}} = \sqrt{2×398,600} \sqrt{\frac{15,000 × 8,000}{15,000 + 8,000}}\) = 64,492.67 km2/s
Using the values of eccentricity and angular momentum, we find the value of rA:
rA = \(\frac{h^2}{\mu} \frac{1}{1 + e\, cos\, \theta_A} = \frac{64,492.67^2}{398,600} \frac{1}{1 + 0.3043\, cos\, 160}\) = 14,613.49 km
From this we will find the corresponding radial and transverse components:
v⊥A = \(\frac{h}{r_A} = \frac{64,492.67}{14,613.49}\) = 4.4132 km/s
vrA = \(\frac{\mu}{h}\) e sin160 = \(\frac{398,600}{64,492.67}\) 0.3043 × sin160 = 0.6433 km/s
Thus the flight path angle is γ = tan-1 \(\frac{v_{\bot_A}}{v_{r_A}}\) = tan-1 \(\frac{0.6433}{2.8388}\) = 12.768 degrees
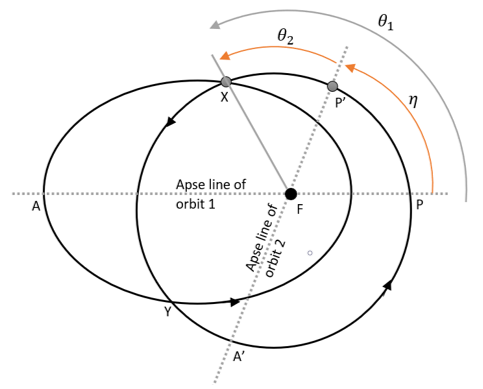
4. What is the formula to compute the rotation of the apse line?
a) η = θ1 – θ2
b) η = θ1 + θ2
c) η = γ1 – γ2
d) η = γ1 + γ2
View Answer
Explanation: The rotation of the line of apsides is given as the difference between the true anomalies of the point of intersection as measured from the periapsis of the orbit. This can ben seen in the figure below.
5. What is the true anomaly of the intersection point X in the orbit 2 if true anomaly of X in orbit 1 is 150 deg? (The given parameters are-e1 = 0.34, e2 = 0.45, h1 = 60,000 km2/s and h2 = 56,000 km2/s)
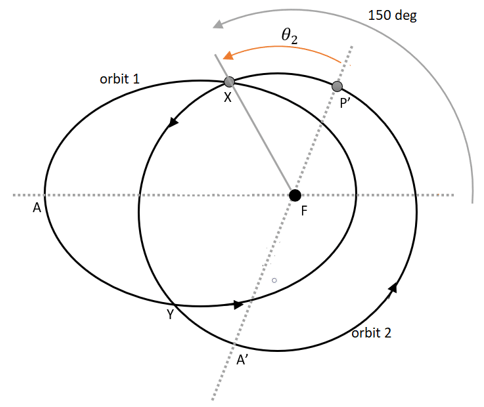
a) 113.15 deg
b) 158.63 deg
c) 145.20 deg
d)165.14 deg
View Answer
Explanation: Given, e1 = 0.25, e2 = 0.45, h1 = 60,000 km2/s and h2 = 56,000 km2/s, θ1 = 150 deg
At the intersection point X, rX1 = rX2
Thus, e1 \(h_1^2\) cosθ1 – e2 \(h_2^2\) cosθ2 = \(h_1^2 – h_2^2\)
0.25 × 60,0002 cos150 – 0.45 × 56,0002 cosθ2 = 60,0002 – 56,0002
-0.9 × 109 – 1.4112 × 109 cosθ2 = 0.464 × 109
cosθ2 = \(\frac{-0.9 × 10^9 – 0.464 × 10^9}{1.4112 × 10^9}\)
θ2 = 165.14 deg
6. What is an apse line?
a) Minor axis
b) Imaginary line connecting the apsides of ellipse
c) Imaginary line connecting the apsides of circular orbit
d) Line tracing the direction of movement of satellite in the orbit
View Answer
Explanation: Apse line is the imaginary line that connects the two extreme apside points in the orbit. It is only defined for elliptic parabolic or hyperbolic orbits as the circular orbit has an eccentricity of 0. For the Non-Hohmann transfer, the two orbits share a common apse line.
7. How many impulses does a Non-Hohmann transfer require?
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: Non-Hohmann transfer makes use of two impulses. The first impulse is made at the initial orbit which helps in entering the transfer orbit. After that, a second impulse is applied to enter the final orbit.
8. True anomalies of θA = 0 and θB = π correspond to the Non-Hohmann transfer.
a) True
b) False
View Answer
Explanation: True anomalies of θA = 0 and θB = π corresponds to the Hohmann transfer. For the Non-Hohmann transfer, the impulse is not given at the apsides (Periapsis, Apsis) thus enabling it to enter a transfer orbit which isn’t tangent to both the initial and the final orbit.
9. What is the value of impulse velocity given to the satellite which has the flight path angle of γ?
a) Δv = \(\sqrt{v_1^2 + v_2^2 – 2v_1 v_2 cos\Delta \gamma}\)
b) Δv = \(\sqrt{v_1^2 + v_2^2 + 2v_1 v_2 cos\Delta \gamma}\)
c) Δv = \(\sqrt{v_1^2 + v_2^2 + 2v_1 v_2 sin\Delta \gamma}\)
d) Δv = \(\sqrt{v_1^2 + v_2^2 – 2v_1 v_2 sin\Delta \gamma}\)
View Answer
Explanation: Whenever there is an impulse given at a point in the orbit which does not lie on the apse line, both the direction and the magnitude of the velocity vector have to be included. Using the vector diagram in the figure given, the change in velocity can be computed at the intersection of orbit 1 and 2.
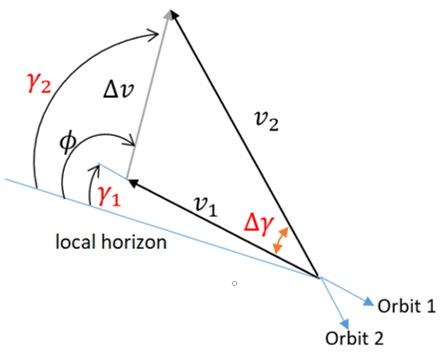
10. What is the angle made by the satellite with the local horizon if the difference between the radial velocity is 2.141 m/s and the difference between its tangential velocity in both the orbits is 0.016 m/s?
a) 55.48 deg
b) 61.21 deg
c) 89.57 deg
d) 74.36 deg
View Answer
Explanation: Given, Δvr = 2.141 m/s, Δv⊥ = 0.016 m/s
The angle Φ which is the the measure of angle between the vector Δ\(\vec{v}\) local horizon is given by:
Φ = tan-1 \(\frac{\Delta v_r}{\Delta v_\perp}\) = tan-1 \(\frac{2.141}{0.016}\)
Φ = 89.57 deg
Sanfoundry Global Education & Learning Series – Orbital Mechanics.
To practice all areas of Orbital Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
