This set of Orbital Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Elliptical Orbits – Set 2”.
1. A satellite orbits the earth with perigee radius of 7,100 km and apogee radius of 69,000 km, what is the time period needed to complete one orbit? Gravitational parameter of earth is 398,600 km3/s2.
a) 20.518 hours
b) 20 hours
c) 11.25 hours
d) 11.214 hours
View Answer
Explanation: Given,
Apogee radius (ra) = 69,000 km
Perigee radius (rp) = 7,100 km
Gravitational Parameter (μ) = 398,600 k3/s2
Semi-major axis (a) = (ra + rp)/2
= (69,000 + 7,100)/2
= 38,050 km
Time period (T) = (2π/μ1/2)a3/2
= (2π/398,6001/2)*38,0503/2
= 73,865.77 s
= 20.518 hours
2. A spacecraft in an elliptical orbit around earth has perigee radius of 7,900 km and apogee radius of 73,000 km, what is its specific energy? Gravitational parameter of earth is 398,600 km3/s2.
a) -5.238 km2/s2
b) -6.231 km2/s2
c) -4.927 km2/s2
d) -2.257 km2/s2
View Answer
Explanation: Given,
Apogee radius (ra) = 73,000 km
Perigee radius (rp) = 7,900 km
Gravitational Parameter (μ) = 398,600 km3/s2
Semi-major axis (a) = (ra + rp) / 2
= (73,000 + 7,900) / 2
= 40,450 km
Specific Energy (ε) = -μ/(2a)
= -398,600*(2*40,450)
= -4.927 km2/s2
3. What is the perigee velocity of a spacecraft in an elliptical orbit if the eccentricity and semi-major axis of the orbit are 0.9 and 50,000 km respectively?
a) 12.307 km/s
b) 2.791 km/s
c) 1.293 km/s
d) 0.648 km/s
View Answer
Explanation: Given,
Gravitational Parameter (μ) = 398,600 km3/s2
Semi-major axis (a) = 50,000 km
Eccentricity (e) = 0.9
From orbit equation for ellipse,
Specific angular momentum (h) = (μa(1 – e2))1/2
= (398,600*50,000*(1-0.92))1/2
= 61,536 km2/s
Perigee radius (rp) = a(1-e)
= 50,000 (1-0.9)
= 5,000 km
Perigee velocity (vp) = h/rp
= 61,536/5,000
= 12.307 km/s
4. What is the eccentricity of an elliptical orbit? Perigee radius is 6,000 km and semi-major axis is 52,910 km.
a) 0.11
b) 0.89
c) 0.41
d) 0.64
View Answer
Explanation: Given,
Perigee radius (rp) = 6,000 km
Semi-major axis (a) = 52,910 km
Eccentricity (e) = 1 – rp / a
= 1 – 6,000 / 52,910
= 0.89
5. What is the true-anomaly-averaged radius when perigee and apogee radius for an elliptical orbit are 10,000 km and 4,000 km?
a) 4,578.91 km
b) 12,000 km
c) 7,000 km
d) 6324.56 km
View Answer
Explanation: Given,
Perigee radius (rp) = 4,000 km
Apogee radius (ra) = 10,000 km
True-anomaly-averaged radius (rmean, θ) = (ra.rp)1/2
= (10,000*4,000)1/2
= 6324.56 km
6. What is the flight path angle at perigee of any elliptical orbit?
a) 90°
b) 0°
c) 180°
d) 270°
View Answer
Explanation: Flight path angle (γ) = atan (esinθ/(1 + ecosθ))
At perigee, true anomaly (θ) = 0°, this implies sinθ = 0
γ = atan (0) = 0°, therefore 0° is the correct answer.
7. The tangential velocity at apogee is ______________ the spacecraft velocity at apogee.
a) equal to
b) less than
c) more than
d) equal to or less than
View Answer
Explanation: Tangential velocity is exactly equal to the spacecraft’s velocity at apogee. True anomaly at the apogee is 180° and as the radial velocity is dependent on the true anomaly as a multiple of sin θ, it should be zero. Therefore, at this instant the tangential velocity and spacecraft’s velocity are the same.
8. Which of the following expressions represent a spacecraft’s resultant velocity in any type of orbit? μ, h, e, θ are gravitational parameter, specific angular momentum, eccentricity and true anomaly respectively.
a) v = \(\frac{\mu}{h} \sqrt{e^2 + 2ecos\theta + 1}\)
b) v = \(\frac{\mu}{h} \sqrt{e^2 + 2ecos\theta + cos^2\theta}\)
c) v = \(\frac{\mu}{h} \sqrt{e^2 \,sin^2\theta}\)
d) v = \(\frac{\mu}{h} \sqrt{2e^2 + 2ecos\theta}\)
View Answer
Explanation:
Tangential velocity vT = \(\frac{h}{r}\)
Substituting orbit equation for r = \(\frac{h^2}{\mu} \frac{1}{1 + ecosθ}\) into the previous equation, we get,
vT = \(\frac{\mu}{h}\)(1 + ecosθ)
vr = \(\frac{\mu}{h}\) esinθ
Spacecraft’s resultant velocity v = \(\sqrt{{v_T}^2 + {v_r}^2}\)
Substituting equations for vT and vr we get,
v = \(\frac{\mu}{h} \sqrt{e^2 sin^2\theta + 1 + 2ecos\theta + e^2 cos^2\theta}\)
v = \(\frac{\mu}{h} \sqrt{e^2 + 2ecos\theta + 1}\), therefore this is the correct expression for spacecraft velocity.
9. The values for x and y are _____________________ respectively. Eccentricity and specific angular momentum are 0.89 and 72,000 km2/s respectively. Gravitational parameter is 398,600 km3/s2.
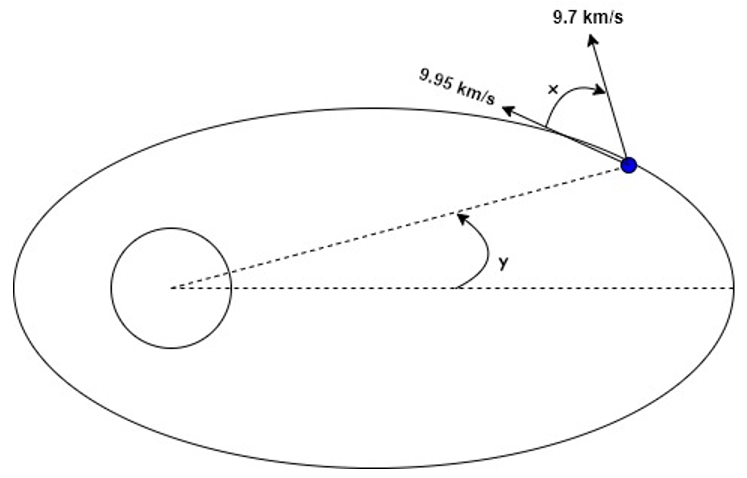
a) 17.14° and 36.48°
b) 20.7° and 44.11°
c) 12.57° and 26.73°
d) 7.77° and 16.31°
View Answer
Explanation: Given,
Satellite velocity (v) = 9.95 km/s
Tangential velocity (vT) = 9.7 km/s
Radial velocity (vr) = (v2 – vT2)1/2
= (9.952 – 9.72)1/2
= 2.216 km/s
Rearranging, radial velocity equation, gives us y (true anomaly)
y = asin((hvr)/(μe))
= asin((72,000*2.216)/(398,600*0.89))
= 26.73°
Now for x (flight path angle),
x = atan (esinx/(1 + ecosx))
= atan (0.89*sin26.73°/(1+0.89*cos26.73°))
= 12.57°
10. What is the spacecraft’s velocity if specific angular momentum of 72,000 km2/s, true anomaly of 17° and eccentricity of 0.89 is measured?
a) 9.11 km/s
b) 14.14 km/s
c) 10.35 km/s
d) 11.28 km/s
View Answer
Explanation: Given,
Specific angular momentum (h) = 72,000 km2/s
True anomaly (θ) = 17°
Eccentricity (e) = 0.89
Spacecraft velocity (v) = (μ/h)√(e2 + 2ecosθ + 1)
= (398,600/72,000)√(0.892 + 2*0.89*cos17° + 1)
= 10.348 km/s
Sanfoundry Global Education & Learning Series – Orbital Mechanics.
To practice all areas of Orbital Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
