This set of Orbital Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Hyperbolic Orbit”.
1. A satellite is travelling in a hyperbolic trajectory of eccentricity 2.5 and specific angular momentum of 87,989 km2/s. What is the hyperbolic excess speed for this trajectory? Standard gravitational parameter is 398,600 km3/s2.
a) 10.38 km/s
b) 10.22 km/s
c) 11.19 km/s
d) 12.56 km/s
View Answer
Explanation: Given,
Specific angular momentum (h) = 87,899 km2/s
Eccentricity (e) = 2.5
Gravitational Parameter (μ) = 398,600 km3/s2
Hyperbolic excess velocity (v∞) = (μ/h)(e2 – 1)1/2
= (398,600/87,989)(2.52 – 1)1/2
= 10.38 km/s
2. What is the periapsis radius of a satellite travelling in a hyperbolic trajectory? The satellite’s speed is two times the hyperbolic excess speed. The eccentricity of the trajectory is 1.2. The radius of satellite from center of earth is 36,613 km.
a) 12,000 km
b) 8,900 km
c) 10,984 km
d) 15,060 km
View Answer
Explanation: Given,
Radius of satellite (r) = 36,613 km
Standard gravitational parameter (μ) = 398,600 km3/s2
Eccentricity (e) = 1.2
We know for hyperbolic trajectories,
(Satellite speed)2 = (Hyperbolic Excess Speed)2 + (Escape Velocity)2
v2 = v∞2 + vesc2
4v∞2 = v∞2 + 2μ/r
3v∞2 = 2μ/r
r = (2μ)/(3v∞2)
We know,
v∞2 = (μ/h)2(e2 – 1)
Substituting back into equation for r, we get,
r = (2/3)(h2/μ)(1/e2 – 1)
Substituting orbit equation for perigee radius, we get,
r = (2/3)(rp/(e – 1))
Therefore, rearranging the equation to get rp
rp = 3r(e-1)/2
= 3*36,613*(1.2-1)/2
= 10,984 km
3. A lunar lander is leaving earth on a hyperbolic trajectory with a perigee altitude of 900 km from earth’s surface. The perigee velocity of the trajectory is 14.3 km/s. What is the hyperbolic excess speed? The radius of earth is 6378 km and its gravitational parameter is 398,600 km3/s2.
a) 10.22 km/s
b) 9.98 km/s
c) 9.74 km/s
d) 10.02 km/s
View Answer
Explanation: Given,
Perigee speed (vp) = 14.3 km/s
Satellite radius (r) = 6378 + 900
= 7278 km
Escape velocity (vesc) = (2μ/r)1/2
= (2*398,600/7278)1/2
= 10.466 km/s
Hyperbolic excess speed (v∞) = (vp2 – vesc2)1/2
= (14.32 – 10.4662)1/2
= 9.744 km/s
4. What is the specific angular momentum of a hyperbolic trajectory with perigee radius of 7278 km and perigee velocity of 20 km/s?
a) 125,981 km2/s
b) 145,560 km2/s
c) 112,134 km2/s
d) 110,156 km2/s
View Answer
Explanation:
Specific angular momentum = Perigee radius x Perigee velocity
= 7278 x 20
= 145,560 km2/s
5. What is the eccentricity of a trajectory with specific angular momentum of 100,170 km2/s and a perigee radius of 6678 km? Gravitational parameter is 398,600 km3/s2.
a) 1.43
b) 1.25
c) 2.15
d) 2.77
View Answer
Explanation: From orbit equation,
Eccentricity (e) = (Specific angular momentum)2/[(gravitational parameter)*(Perigee radius)] – 1
= [100,1702/(398,600*6678)] – 1
= 2.769
6. What is the true anomaly of a satellite relative to earth if it has an eccentricity of 2.9? The radius of the satellite is 49,500 km and the perigee radius is 6888 km. Gravitational parameter is 398,600 km3/s2.
a) 112°
b) 107°
c) 99°
d) 102°
View Answer
Explanation: Orbit equation for perigee gives us,
h = [rpμ(1 + e)]1/2
= [6888*398,600*(1 + 2.9)]1/2
= 103,477.88 km2/s
From general orbit equation
True Anomaly, θ = acos[(1/e)(h2/(μr) – 1)]
= acos[(1/2.9)(103,477.82/(398,600*49,500) – 1)]
= 99.07
7. What is the radial velocity of a satellite at a true anomaly of 100°? The eccentricity of this trajectory is 2.3 and perigee radius is 6778 km.
a) 9.562 km/s
b) 9.122 km/s
c) 8.221 km/s
d) 10.24 km/s
View Answer
Explanation: Given,
Perigee radius (rp) = 6778 km
Eccentricity (e) = 2.3
True anomaly (θ) = 100°
From the orbit equation,
Specific angular momentum (h) = [μrp(1 + e)]1/2
= [398,600*6778*(1 + 2.3)]1/2
= 94,422.69 km2/s
Radial velocity (vr) = (μ/h)esin(θ)
= (398,600/94,422.69)*2.3*sin(100°)
= 9.562 km/s
8. _______________ energy is the energy divided by mass required to escape the gravitational pull of any massive body.
a) Characteristic
b) Specific
c) Excess
d) Dynamic
View Answer
Explanation: Characteristic energy or specific excess energy of a hyperbolic orbit is the energy required to escape. Specific energy on its own is a measure of a spacecraft’s total energy divided by its mass. Characteristic energy times mass is excess energy of a spacecraft, but the question asks for energy divided by mass. While, dynamic energy is not a term used in orbital mechanics.
9. What is the eccentricity of a meteoroid approaching earth as shown in the diagram below? Gravitational parameter is 398,600 km3/s2.
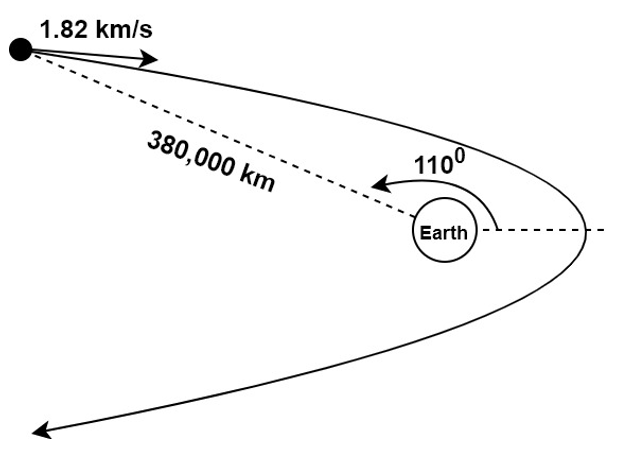
a) 1.78
b) 1.28
c) 1.11
d) 2.13
View Answer
Explanation: Given,
Meteoroid speed (v) = 1.82 km/s
Meteoroid radius from earth (r) = 380,000 km
True anomaly (θ) = 110°
From conservation of energy,
Specific Energy (ε) = v2/2 – μ/r
= 1.822/2 – 398,600/380,000
= 0.6073 km2/s2
From e-h-ε relation,
h2 = -(1/2)(μ2/ε)(1-e2)
h2 = (1/2)(398,6002/0.6073)(e2-1)
h2 = 1.3081 x 1011(e2-1)
From orbit equation,
h2 = μr(1 + ecosθ)
h2 = 398,600*380,000*(1 + ecos110°)
h2 = (-0.51805e + 1.51468) x 1011
Equating both equations,
1.3081(e2-1) = -0.51805e + 1.51468
e2 + 0.396e – 2.1579 = 0
Solving the equation for positive root,
e = 1.28
10. What is the turn angle of a hyperbolic trajectory with eccentricity 1.2?
a) 45.32°
b) 12.45°
c) 56.44°
d) 41.24°
View Answer
Explanation: Given,
Eccentricity (e) = 1.2
Turn angle = 2*asin(1/e)
= 2*asin(1/1.2)
= 56.44°
Sanfoundry Global Education & Learning Series – Orbital Mechanics.
To practice all areas of Orbital Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
