This set of Orbital Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Orbits”.
1. Given, the semi-major axis and semi-minor axis are 6580 km and 5910 km respectively, what is the eccentricity of the orbit?
a) 0.89
b) 0.44
c) 0.64
d) 0.25
View Answer
Explanation: Given,
Semi-major axis (a) = 6580 km
Semi-minor axis (b) = 5910 km
Eccentricity (e) = (1 – (b/a)2)1/2
= (1-(5910/6580)2)1/2
= 0.44
2. What is the eccentricity of a spacecraft around earth? Given, specific energy is -10.29 km2/s2, specific angular momentum is 10,112 km2/s. The standard gravitational parameter of earth is 398,600 km3/s2.
a) 0.478
b) 1.45
c) 0.691
d) 0.456
View Answer
Explanation: Given,
Specific energy (ε) = -10.29 km2/s2
Specific angular momentum (h) = 10,112 km2/s
Standard gravitational parameter (μ) = 398,600 km3/s2
Using the e-h-ε relation
e = (1+(2εh)/μ)1/2
= (1+(2*-10.29*10,112)/398,600)1/2
= 0.691
3. Which of the following orbit shapes will be formed if a satellite is travelling at exactly the escape velocity of earth?
a) Circular
b) Parabolic
c) Hyperbolic
d) Elliptical
View Answer
Explanation: Parabolic orbits are formed at the exact escape velocity of a planet. Elliptical and circular orbits are formed when the satellite’s velocity is less than the escape velocity. Whereas, at velocities higher than the escape velocity, hyperbolic orbits are formed.
4. If the standard gravitational parameter of earth, μ is 398,600 km3/s2 and the radius of earth is 6378 km, what is the period of a satellite revolving around earth in a circular orbit 500 kms above the surface of the earth?
a) 2,012.2 s
b) 5,801.06 s
c) 1,156.21 s
d) 937.267 s
View Answer
Explanation: The Time Period of a circular orbit can be derived as:
T = (2πR3/2/√(μ)
R = radius of earth + distance from the surface of earth to satellite
R = 6378 + 500
R = 6978 km
Therefore, T = (2π(6978)3/2/√(398600)
T = 5,801.06 s
5. The eccentricity of an asteroid is 0.7. What is the shape of its orbit around the sun?
a) Circular
b) Hyperbolic
c) Parabolic
d) Elliptical
View Answer
Explanation: Elliptical orbits have an eccentricity greater than zero and less than one. Most planets and orbits orbiting around the sun are elliptical in shape.
6. What is the eccentricity of a satellite around a planet if the periapsis and apoapsis are at 6,778 km and 10,378 km respectively from the center of the planet?
a) 0.7051
b) 0.5
c) 0.2098
d) 0.901
View Answer
Explanation: The eccentricity of an orbit can be determined as follows:
e = (Apoapsis distance – Periapsis distance) / (Apoapsis distance + Periapsis distance)
e = (10,378 – 6778) / (10,378 + 6778)
e = 0.2098
7. What is the semi-major axis of an elliptical orbit with perigee and apogee distances of 2500 km and 8000 km respectively?
a) 5250 km
b) 5000 km
c) 4950 km
d) 5150 km
View Answer
Explanation: Semi-major axis of an ellipse is half of the major axis. Major axis can be represented as a sum of perigee and apogee distances. Therefore,
Semi-major axis = (2500 + 8000) / 2 = 5,250 km
8. Which of the following describes the angle measured between the ascending node and the periapsis?
a) Argument of periapsis
b) Inclination
c) Longitude of the ascending node
d) True anomaly
View Answer
Explanation: Argument of periapsis is defined as the angle between ascending node and periapsis. The angle between vernal equinox and ascending node is longitude of the ascending node. The angle between earth’s equatorial plane unit vector and satellite’s angular momentum vector is inclination. True anomaly is the angle between perigee and spacecraft position relative to center of the earth.
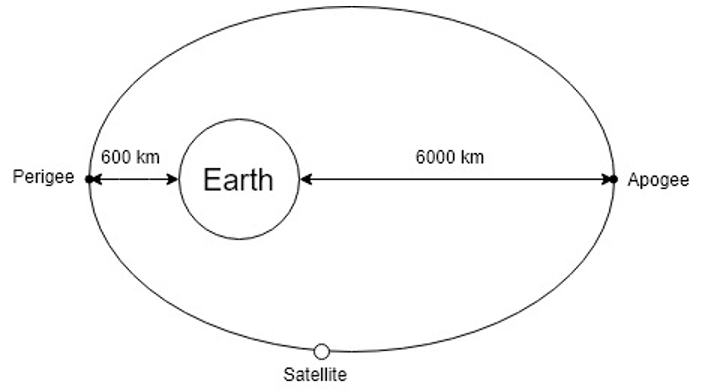
9. What is the specific angular momentum, h of a satellite in orbit as shown in figure below? Given, radius of earth is 6378 km and standard gravitational parameter is 398,600 km3/s2.
a) 44,342 km2/s
b) 59,642 km2/s
c) 57,112 km2/s
d) 12,012 km2/s
View Answer
Explanation: Perigee distance, rp = Radius of earth + distance from surface
= 6378 + 400
= 6978 km
Similarly, Apogee distance, ra = 6378 + 6000
=12,378 km
Eccentricity, e = (ra – rp) / (ra + rp)
= (12,378 – 6,978) / (12,378 + 6,978)
= 0.2789
From Keplerian solution to two-body problems, Angular momentum, h can be found:
r = (h2 / μ) / (1 + e.cosθ)
For perigee, θ = 0 degrees
Therefore, rp = (h2 / μ) / (1 + e)
h = √(rp (1 + e) μ)
h = √(6978 x (1 + 0.2789) x 398,600)
h = 59,642 km2/s
10. Which of the following coordinate systems has sun as its center?
a) Geocentric-Equatorial System
b) Geocentric-Ecliptic System
c) Heliocentric-Ecliptic System
d) Right Ascension-declination System
View Answer
Explanation: Heliocentric-Ecliptic system is a system which has sun as its center or origin. Fundamental plane of operation of this coordinate system is ecliptic plane of our solar system. Most of the planets along with the sun lie on this plane.
Sanfoundry Global Education & Learning Series – Orbital Mechanics.
To practice all areas of Orbital Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
