This set of Orbital Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Time of Flight”.
1. Which scientist determined the relationship between the orbital position and time of flight?
a) Johannes Kepler
b) Ptolemy
c) Nicolas Copernicus
d) Tycho Brahe
View Answer
Explanation: Time of flight which is the transit time between two positions in an orbit was found out by Johannes Kepler. He found out the relation between the orbital position and time of flight which came to be known as Kepler’s equation.
2. What is the ratio of area swept by the object and the corresponding time of flight equal to?
a) h
b) h/2
c) h/3
d) 2h
View Answer
Explanation: According to the figure below, the rate of area swept by the radius vector is always a constant. This is h/2. Where A1 is the area swept by the planet by moving from periapsis to point P. The relation is given by:
\(\frac{dA}{dt} = \frac{h}{2}\)
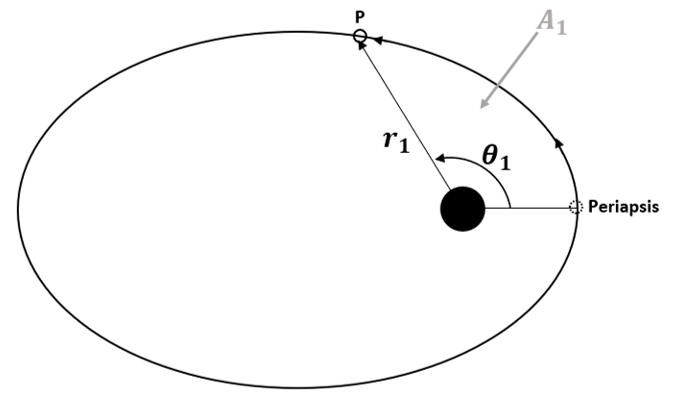
3. The time of flight is less than one period.
a) True
b) False
View Answer
Explanation: Since the area ratio (Swept area by total area of ellipse) is less than one, the time of flight is also less than one period. The relation is as below:
t1 – tp = \(\frac{A_1}{A_{ellipse}}\) Tperiod
Where, t1 is the time at point 1 in the orbit, tp is the time at the perigee, A1 is the area swept by the object in the orbit on reaching point 1, Aellipse is the total area of the elliptical orbit, Tperiod is the orbital time period.
4. Which of the angles defined by Kepler is used to obtain the position of the body using the auxiliary circle?
a) Eccentric anomaly
b) True anomaly
c) Mean anomaly
d) Eccentricity
View Answer
Explanation: Eccentric anomaly is the angle that is formed by drawing an auxiliary circle of an ellipse with center O and focus F. A perpendicular line is drawn to the semimajor axis intersecting at A. The angle E thus formed is the eccentric anomaly. It is used to obtain the position of the body in the orbit.
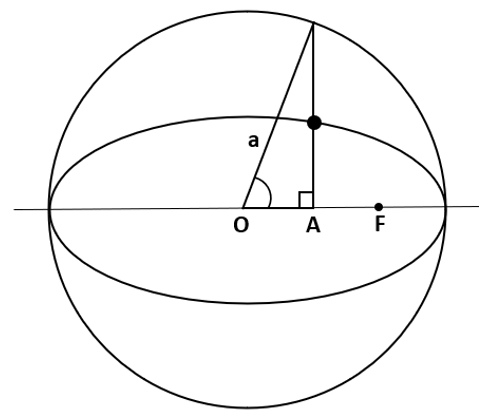
5. Which of these equations show the relation between the true anomaly and eccentric anomaly?
a) tan \(\frac{\theta}{2} = \sqrt{\frac{1 – e}{1 + e}}\) tan \(\frac{E}{2}\)
b) sin \(\frac{E}{2} = \sqrt{\frac{1 – e}{1 + e}}\) sin \(\frac{\theta}{2}\)
c) tan \(\frac{E}{2} = \sqrt{\frac{1 + e}{1 – e}}\) tan \(\frac{\theta}{2}\)
d) tan \(\frac{E}{2} = \sqrt{\frac{1 – e}{1 + e}}\) tan \(\frac{\theta}{2}\)
View Answer
Explanation: The formula for half-angle tangent is:
tan \(\frac{\theta}{2} = \frac{sin\theta}{1 + cos\theta} = \frac{\frac{\sqrt{1 – e^2 sinE}}{1 -ecosE}}{1 + \frac{cosE – e}{1 – ecosE}}\)
tan \(\frac{\theta}{2} = \frac{\sqrt{1 – e^2 sinE}}{1 – ecosE + cosE – e} = \sqrt{\frac{1 + e}{1 – e}}\) tan \(\frac{E}{2}\)
Thus, tan \(\frac{E}{2} = \sqrt{\frac{1 – e}{1 + e}}\) tan \(\frac{\theta}{2}\)
6. A satellite is orbiting the earth in a geocentric orbit of perigee radius = 6,500 km and apogee radius of 9,800 km. What is the approximate time taken to fly from perigee to true anomaly of 100 deg?
a) 200 sec
b) 550 sec
c) 900 sec
d) 1000 sec
View Answer
Explanation: Given, ra = 9,800 km, rp = 6,500 km, θ = 100 deg
Eccentricity is calculated by:
e = \(\frac{r_a – r_p}{r_a + r_p} = \frac{9,800 – 6,500}{9,800 + 6,500}\) = 0.202
Angular momentum is given by:
rp = \(\frac{h^2}{\mu} \frac{1}{1 + ecos\theta_p}\)
6,500 = \(\frac{h^2}{398,600} \frac{1}{1 + 0.202cos0}\)
h = 46,427.264 km2/s
Time period of the orbit is calculated by:
T = \(\frac{2\pi}{\mu^2} \Big(\frac{h}{\sqrt{1 – e^2}} \Big)^3 = \frac{2\pi}{398,600^2} \Big(\frac{46,427.264}{\sqrt{1 – 0.202^2}}\Big)^3\) = 4,212.73 sec
Using the relation between true anomaly and eccentric anomaly:
tan \(\frac{E}{2} = \sqrt{\frac{1 – e}{1 + e}}\) tan \(\frac{\theta}{2}\) = \(\sqrt{\frac{1-0.202}{1+0.202}}\) tan \(\frac{100}{2}\) = 0.971
tan \(\frac{E}{2}\) = 0.971
E = 2 × tan-1 0.971 = 88.314 deg = 1.5414 rad
Using Kepler’s equation:
Me = E – esinE = 1.5414 – 0.202 × sin1.5414 = 1.339 rad
Thus, the time taken to reach point at true anomaly of 100 deg is:
t = \(\frac{M_e}{2\pi}\) T = \(\frac{1.339}{2\pi}\) 4,212.73 = 897.768 sec ≅ 900 sec.
7. What is the imaginary angle between the periapsis point and the imagined position of an object for the same elapsed time called?
a) Eccentric anomaly
b) True anomaly
c) Mean anomaly
d) Eccentricity
View Answer
Explanation: The mean anomaly is an angle an imaginary satellite would have if it were in a circular orbit around the center point O with a time period T equal to the true satellite orbit. It is given by the Kepler’s relation:
Me = E – esinE
8. What is the value of mean motion of the satellite orbiting the earth with an orbit having semi- major axis of 8,500 km?
a) 6.45 × 10-4 rad/s
b) 8.05 × 10-4 rad/s
c) 10.18 × 10-4 rad/s
d) 15.78 × 10-4 rad/s
View Answer
Explanation: Given, a = 8,500 km
The Mean Motion (n) is defined as the number of orbits the satellite completes about the Earth in exactly 24 hours (one solar day).
The formula to calculate the mean motion is: n = \(\sqrt{\frac{\mu}{a^3}} = \sqrt{\frac{398,600}{8,500^3}}\) = 8.05 × 10-4 \(\frac{rad}{s}\).
9. Which of the equations determines the time of flight for a parabolic trajectory?
a) Barker’s equation
b) Euler’s equation
c) Kepler’s equation
d) Madelung equation
View Answer
Explanation: Barker’s equation is used to determine the time of flight from periapsis to a position on the parabolic trajectory at a true anomaly of θ. It is a dimensionless quantity given by:
2\(\sqrt{\frac{\mu}{p^3} (t – t_p) = B + \frac{1}{3} B^3}\)
10. What is the fraction of period required to travel 1/6th of an orbit beyond perigee at true anomaly of 60 deg with eccentricity of an orbit = 0.15?
a) 0.8741
b) 0.3004
c) 0.2014
d) 0.1276
View Answer
Explanation: Given, e = 0.15, θ = 60 deg
Relation of eccentric anomaly is:
cosE = \(\frac{cos\theta + e}{1 + ecos\theta} = \frac{cos60 + 0.15}{1 + 0.15 × cos60}\) = 0.60465
E = cos-1 0.60465 = 0.9215 rad
Mean anomaly is given by:
M = E – esinE = 0.9215 – 0.15 × sin0.9215 = 0.802
Ratio of time since perigee passage and time period of the orbit is given by:
\(\frac{t}{P} = \frac{M}{2\pi} = \frac{0.802}{2\pi}\) = 0.1276.
Sanfoundry Global Education & Learning Series – Spaceflight Mechanics.
To practice all areas of Orbital Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
