This set of Orbital Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Hohmann Transfer”.
1. Which of these orbital transfers is the most energy efficient?
a) Bi-elliptic transfer
b) One tangent-burn transfer
c) Hohmann transfer
d) Non-Hohmann transfer
View Answer
Explanation: Hohmann transfer is considered at the most energy efficient two-impulse transfer. It does not truly exist. In this, both the initial and final orbital planes are coplanar and the change in velocity magnitude is tangential to both the initial and final orbits.
2. How many velocity increments are required to carry out the Hohmann transfer?
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: Two velocity increments in total are required to carry out Hohmann transfer. The first velocity increment is done at the inner circular orbit in the direction of the spacecraft. This places it in a higher energy elliptical trajectory. Once reaching the perigee of the elliptical orbit, the second velocity increment is carries out using thrusters to place it in the outer circular orbit.
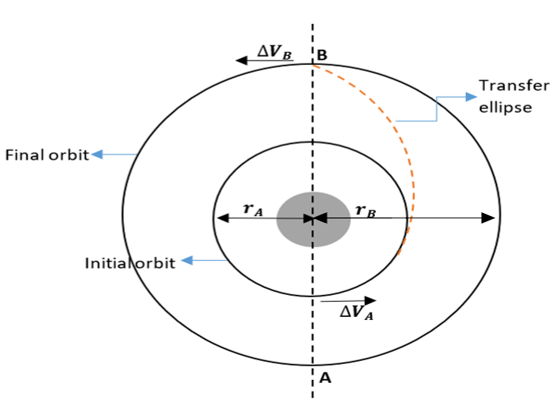
3. What is the velocity change required to perform a Hohmann transfer to a circular orbit at geosynchronous altitude of 35,768 km if the spacecraft is in an initial circular orbit at an altitude of 200 km?
a) 1.874
b) 2.894
c) 3.933
d) 4.784
View Answer
Explanation: Given values are: rA = (6,378 + 200)km = 6,578 km (Where radius of Earth of 6,578 km has to be added)
rB = 35,786 + 6,328 = 42,164 km
Velocity of the initial circular orbit at point A(viA) is:
(viA) = \(\sqrt{\frac{\mu}{r_A}} = \sqrt{\frac{398,600}{6,578}}\) = 7.784 km/s
Semi major axis of the transfer elliptical orbit is given by:
atx = \(\frac{r_A + r_B}{2} = \frac{6,578 + 42,164}{2}\) = 24,372 km
Velocity at the perigee of the transfer orbit is:
vtxA = \(\sqrt{\mu(\frac{2}{r_A} – \frac{1}{a_{tx}})} = \sqrt{398,600(\frac{2}{6,578} – \frac{1}{24,372})}\) = 10.239 km/s
Velocity at the apogee of the transfer orbit is:
vtxB = \(\sqrt{\mu(\frac{2}{r_B} – \frac{1}{a_{tx}})} = \sqrt{398,600(\frac{2}{42,164} – \frac{1}{24,372})}\) = 1.579 km/s
Velocty of final circular orbit:
vfB = \(\sqrt{\frac{\mu}{r_B}} = \sqrt{\frac{398,600}{42,164}}\) = 3.075 km/s
Velocity imparted to change the initial circular orbit to transfer orbit:
ΔvA = vtxA – viA = 10,239 – 7,784 = 2.455 km/s
Velocity imparted to change transfer orbit to the final circular orbit:
ΔvB = vfB – vtxB = 3,075 – 1,597 = 1.478 km/s
Total velocity requires to do the total orbital manouver:
vT = ΔvA + ΔvB = 2.455 + 1.478 = 3.933\(\frac{km}{s}\).
4. What is the time period of the transfer ellipse for a vehicle which is moving in a hyperbolic trajectory at an altitude of 6000km moving at 15 km/s whos speed is eventually slowed to enter a 600 km altitud circular orbit.
a) 2,674.1 s
b) 4,659.3 s
c) 8,450.0 s
d) 9,475.2 s
View Answer
Explanation: In order to calculate the time period (T2) of the transfer orbit we find eccentricty and angular momentum.
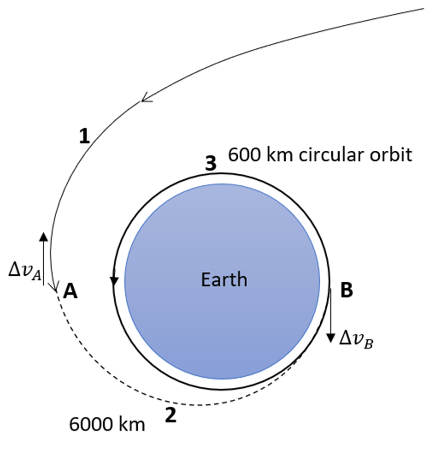
Given: rA = (6,378 + 6,000) km = 12,378 km
rB = (6,378 + 600) km = 6,978 km
In order to find the eccentricity of transfer orbit:
e2 = \(\frac{r_A – r_B}{r_A + r_B} = \frac{12,378 – 6,978}{12,378 + 6,978}\) = 0.27898
Angular momentum at the perigee is:
rB = \(\frac{h_2^2}{\mu} \frac{1}{1 + e_2}\)
6978 = \(\frac{h_2^2}{398,600} \frac{1}{1 + 0.27898}\)
h2 = 59,643.9 km2/s
To calculate the time period of the transfer orbit we use the formula as given below:
T2 = \(\frac{2\pi}{\mu^2}(\frac{h_2}{\sqrt{1 – e_2^2}})^3 = \frac{2\pi}{398,600^2} (\frac{59,643.9}{\sqrt{1 – 0.27898^2}})^3\) = 9,475.2 s
5. How many burns are required to successfully carry out Bi-Elliptical Hohmann transfer?
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: In order to carry out Bi-Elliptical Hohmann tranfer 3 burns are required. 1st burn is to convert the circular orbit at r1 to elliptical orbit with perigee rp = r1 and apogee ra = r*. The second burn is carried out at the apogee to raise the perigee of elliptical orbit to r2. Finally at perigee, the orbit is circulized by lowering the perigee to r2.
6. The radius of the elliptical orbit in bi-elliptical hohmann transfer is a free entity.
a) True
b) False
View Answer
Explanation: r* is a free parameter and can have any value. Usually as r* tends to infinity, the bi-elliptic tranfer becomes more efficient. As r* tends to infinity, time tends to infinity so there is trade-off between time and efficiency.
7. If a satellite is orbiting at an altitude of 350 km at an inclination of 15 degrees, what is the total veloicty change which is required to tranfer the satellite from the initial circular orbit to a geosynchronous orbit at 0 degrees inclination using Hohmann transfer?
a) 4.887 km/s
b) 5.334 km/s
c) 8.978 km/s
d) 3.145 km/s
View Answer
Explanation: The given values in th questions are:
rA = (6,378 + 350)km = 6,728 km
rB = (6,378 + 35,786)km = 42,164 km (Where Geosynchronous altitude is 35,786 km)
i = 15°
To calculate the semi-major axis of the transfer ellipse:
atx = \(\frac{r_A + r_B}{2} = \frac{6,728 + 42,164}{2}\) = 24,446 km
Finding the initial velocity at point A:
(viA) = \(\sqrt{\frac{\mu}{r_A}} = \sqrt{\frac{398,600}{6,728}}\) = 7.697 km/s
Fiding the final velocity at point B:
vfB = \(\sqrt{\frac{\mu}{r_B}} = \sqrt{\frac{398,600}{42,164}}\) = 3.075 km/s
Finding the velocity on transfer orbit at final point (B):
vtxB = \(\sqrt{μ(\frac{2}{r_B} – \frac{1}{a_{tx}})} = \sqrt{398,600(\frac{2}{42,164} – \frac{1}{24,446})}\) 1.613 km/s
Finding the velocity on transfer orbit at final orbit (A):
vtxA = \(\sqrt{μ(\frac{2}{r_A} – \frac{1}{a_{tx}})} = \sqrt{398,600(\frac{2}{6,728} – \frac{1}{24,446})}\) = 10.109 km/s
Initial velocity change:
ΔvA = vtxA – viA = 10.109 – 7.697 = 2.412 km/s
Final velocity change:
ΔvB = \(\sqrt{{v_{txB}}^2 + {v_{fB}}^2 – 2 × v_{txB} × v_{fB} × cos i}\)
ΔvB = \(\sqrt{1.613^2 + 3.075^2 – 2 × 1.613 × 3.075 × cos (15)}\) = 2.475 km/s
Δvtotal = ΔvA + ΔvB = 2.412 + 2.475 = 4.887\(\frac{km}{s}\).
8. What is the shape of the transfer orbit in the Hohmann transfer?
a) Circular
b) Elliptical
c) Parabolic
d) Hyperbolic
View Answer
Explanation: The Hohmann transfer involves tranfer of the object/satellite between two circular orbits using a transfer elliptical orbit. When transfering from a smaller orbit to a larger one, the change in velocity is applied in the direction of motion. Transfer orbits cannot take the shapes of Parabolic or Hyperbolic as they are usually escapy trajectories.
9. What is the time period of the transfer orbit in Hohmann transfer?
a) Same as the period of orbit
b) Half of the period of orbit
c) Twice of the period of orbit
d) One-third of the period of orbit
View Answer
Explanation: The transfer time is half of the period of orbit. Δt = \(\frac{T}{2} = \pi\sqrt{\frac{a^3}{\mu}}\)
Δt = \(\sqrt{\frac{(r_1 + r_2)^3}{2\mu}}\)
10. The Hohmann transfer is carried out for perpendicular elliptic orbits.
a) True
b) False
View Answer
Explanation: The Hohmann transfer is carried out between two circular co-planer orbits. The tranfer orbit is the elliptical orbit. The co-planer orbits result in optimising energy.
Sanfoundry Global Education & Learning Series – Orbital Mechanics.
To practice all areas of Orbital Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
