This set of Orbital Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Elliptical Orbits”.
1. A satellite orbits the earth with perigee radius of 7,500 km and apogee radius of 77,000 km, what is its eccentricity?
a) 0.822
b) 0.412
c) 0.251
d) 0.99
View Answer
Explanation: Given,
Apogee radius (ra) = 77,000 km
Perigee radius (rp) = 7,500 km
Eccentricity (e) = (ra – rp) / (ra + rp)
= (77,000 – 7,500) / (77,000 + 7,500)
= 0.822
2. A spacecraft in an elliptical orbit around earth has perigee radius of 7,900 km and apogee radius of 73,000 km, what is its semi-major axis?
a) 12,000 km
b) 8,900 km
c) 40,450 km
d) 15,060 km
View Answer
Explanation: Given,
Apogee radius (ra) = 73,000 km
Perigee radius (rp) = 7,900 km
Semi-major axis (a) = (ra + rp) / 2
= (73,000 + 7,900) / 2
= 40,450 km
3. What is the specific angular momentum of an Iridium satellite if the orbit is in an elliptical orbit that has a semi-major axis and eccentricity of 46,000 km and 0.85 respectively. Gravitational parameter of earth is 398,600 km3/s2?
a) 71,331 km2/s
b) 68,000 km2/s
c) 77,000 km2/s
d) 98,000 km2/s
View Answer
Explanation: Given,
Gravitational Parameter (μ) = 398,600 km3/s2
Semi-major axis (a) = 46,000 km
Eccentricity (e) = 0.85
From orbit equation for ellipse,
Specific angular momentum (h) = (μa(1-e2))1/2
= (398,600*46,000*(1-0.852))1/2
= 71,331 km2/s
4. What is the tangential velocity of a satellite at an altitude of 1,100 km from earth’s surface? Specific angular momentum is 72,000 km2/s.
a) 11.01 km/s
b) 9.63 km/s
c) 7.71 km/s
d) 7.89 km/s
View Answer
Explanation: Given,
Specific angular momentum (h) = 72,000 km2/s
Satellite radius (r) = Earth’s radius + distance from Earth surface
= 6378 + 1,100
= 7478 km
Tangential velocity (vT) = h/r
= 72,000/7,478
= 9.63 km/s
5. What is the true anomaly of a satellite around earth if specific angular momentum is 72,000 km2/s, altitude is 1,100 km, eccentricity is 0.89 and radial velocity is 2 km/s?
a) 14.35°
b) 12.15°
c) 20.15°
d) 23.95°
View Answer
Explanation: Given,
Specific angular momentum (h) = 72,000 km2/s
Eccentricity (e) = 0.89
Radial velocity (vr) = 2 km/s
Gravitational Parameter (μ) = 398,600 km3/s2
Rearranging radial velocity formula,
True anomaly (θ) = asin [(hvr) / (μe)]
= asin [(72,000*2) / (398,600*0.89)]
= 23.95°
6. What is the apogee velocity of a spacecraft in an elliptical orbit if the eccentricity and semi-major axis of the orbit are 0.9 and 50,000 km2/s respectively?
a) 12.307 km/s
b) 2.791 km/s
c) 1.293 km/s
d) 0.648 km/s
View Answer
Explanation: Given,
Gravitational Parameter (μ) = 398,600 km3/s2
Semi-major axis (a) = 50,000 km
Eccentricity (e) = 0.9
From orbit equation for ellipse,
Specific angular momentum (h) = (μa(1-e2))1/2
= (398,600*50,000*(1-0.92))1/2
= 61,536 km2/s
Apogee radius (ra) = a(1 + e)
= 50,000 (1 + 0.9)
= 95,000 km
Apogee velocity (va) = h/ra
= 61,536/95,000
= 0.6477 km/s
7. What is the semi-major axis of an elliptical orbit with apogee and perigee radius of 100,000 km and eccentricity 0.89?
a) 52,910 km
b) 55,000 km
c) 71,000 km
d) 12,012 km
View Answer
Explanation: Given,
Apogee radius (ra) = 100,000 km
Eccentricity (e) = 0.89
Semi-major axis (a) = ra / (1 + e)
= 100,000 / (1 + 0.89)
= 52,910 km
8. What is the average distance between the earth and a satellite for one complete orbit also known as?
a) Perigee radius
b) Satellite radius
c) Apogee radius
d) True-anomaly-averaged radius
View Answer
Explanation: True-anomaly-averaged radius is the average distance between satellite and earth for one complete orbit. To find the average distance between the earth and a satellite, the total true anomaly angle of 2π is divided into n equal segments with Δθ, and a sum of satellite radiuses is calculated from every nth interval. The sum is then divided by n. To make the solution easier, the sum is written as an integral and solved.
9. What is the true anomaly of the satellite as shown? The eccentricity of the orbit is 0.85.
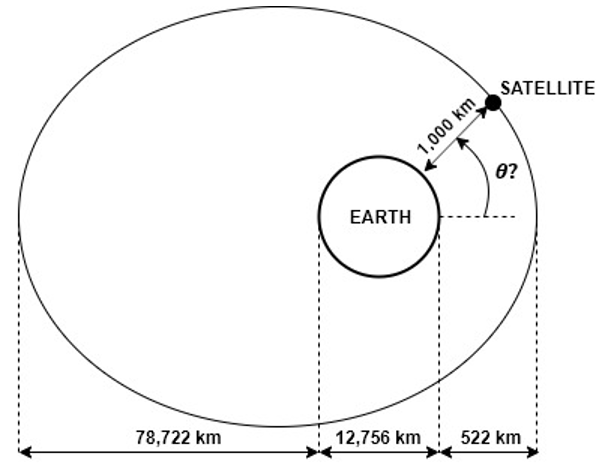
a) 23.796°
b) 30.796°
c) 37.706°
d) 21.791°
View Answer
Explanation: Given,
Satellite radius (r) = 1,000 + 12,756/2
= 7,378 km
Semi-major axis (a) = (78,722 + 12,756 + 522)/2
= 46,000 km
Eccentricity (e) = 0.85
Rearranging the orbit equation for true anomaly (θ) we get,
θ = acos[(1/e)(a(1 – e2)/r – 1)]
= acos[(1/0.85)(46,000(1 – 0.852)/7,378 – 1)]
= 30.796°
10. The eccentricity of an elliptical orbit is 0.9, what is the maximum flight path angle for this orbit?
a) 45.32°
b) 64.16°
c) 50.44°
d) 43.24°
View Answer
Explanation: We know,
Flight path angle (γ) = tan-1\((\frac{esinθ}{1 + ecosθ})\), where θ is the true anomaly and e is eccentricity
At \(\frac{d\gamma}{d\theta}\) = 0 is where the maximum flight path angle is
Therefore, \(\frac{d}{d\theta}\) [tan-1\((\frac{esinθ}{1 + ecosθ})\)] = 0
\(\frac{1}{1 + (\frac{esin\theta}{1 + ecos\theta})^2} \frac{d}{d\theta} (\frac{esin\theta}{1 + ecos\theta})\) = 0
\(\frac{e(e + cos\theta)}{(1 + ecos\theta)^2 + e^2\, sin^2 \theta}\) = 0
The expression will be equal to zero if cosθ = -e
For maximum γ, θ = cos-1(-e) = cos-1(-0.9) = 154.16°
Maximum Flight path angle (γmax) = tan-1\((\frac{0.9sin154.16}{1 + 0.9cos154.16})\) = 64.16°
Sanfoundry Global Education & Learning Series – Orbital Mechanics.
To practice all areas of Orbital Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
