This set of Spaceflight Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Path of Ballistic Missiles”.
1. Which of these conic orbits is followed by the free flight trajectory?
a) Circular
b) Elliptical
c) Parabolic
d) Hyperbolic
View Answer
Explanation: Ballistic missile trajectory is composed of three regimes-powered flight, free-flight and re-entry portion. Free-flight portion is the only part of the trajectory that follows a conic orbit. It constitutes most of the trajectory path. During free-flight the trajectory is part of a conic orbit-almost always an ellipse which is symmetrical.
2. Which of these equations represent the free-flight range equation?
a) cos \(\frac{\psi}{2} = \frac{1-Q_{bo} sin^2 \phi_{bo}}{\sqrt{1 + Q_{bo} (Q_{bo} – 2)sin^2 \phi_{bo}}}\)
b) cos \(\frac{\psi}{2} = \frac{1+Q_{bo} cos^2 \phi_{bo}}{\sqrt{1 + Q_{bo} (Q_{bo} + 2)cos^2 \phi_{bo}}}\)
c) cos \(\frac{\psi}{2} = \frac{1-Q_{bo} cos^2 \phi_{bo}}{\sqrt{1 + Q_{bo} (Q_{bo} – 2)cos^2 \phi_{bo}}}\)
d) cos \(\frac{\psi}{2} = \frac{1-Q_{bo} cos^2 \phi_{bo}}{\sqrt{1 + Q_{bo} (Q_{bo} – 2)sin^2 \phi_{bo}}}\)
View Answer
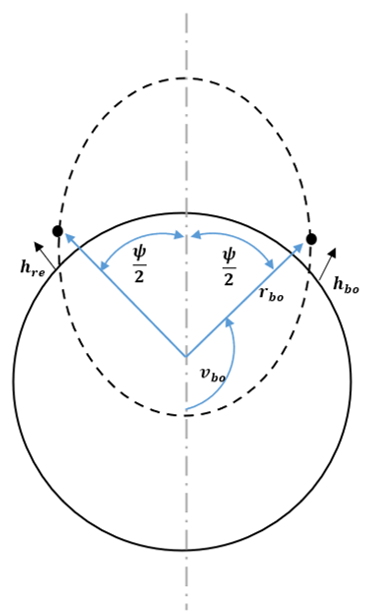
Explanation: From the figure, the equation of conic id applied in the free-flight range:
rbo = \(\frac{p}{1 + e \,cosv_{bo}}\)
Transferring cosvbo to one side: cosvbo = \(\frac{p-r_{bo}}{er_{bo}}\)
The free flight trajectory is assumed to be symmetrical which results in hbo = hre
Thus, cos \(\frac{\psi}{2}\) = -cosvbo
cos \(\frac{\psi}{2}\) = \(\frac{r_{bo} – p}{er_{bo}}\) → 1
Using the formula of p = \(\frac{h^2}{\mu}\) and h = rv cosΦ
This results in p = \(\frac{r^2 v^2 cos^2 \phi}{\mu}\) = rQ cos2 Φ → 2
Using the relation of semi latus rectum and eccentricity: p = a(1 – e2)
e2 = 1 – \(\frac{p}{a}\) → 3
a = \(\frac{r}{2-Q}\) → 4
Substituting equation 2 and 4 in equation 3, we get:
e2 = 1 + Q(Q – 2) cos2 Φ → 5
Finally, we substitute equation 2 and 5 in equation 1 to get the free flight range equation:
cos \(\frac{\psi}{2} = \frac{1-Q_{bo} cos^2 \phi_{bo}}{\sqrt{1 + Q_{bo} (Q_{bo} – 2)cos^2 \phi_{bo}}}\)
3. What is the free-flight range angle if the re-entry angle and powered flight range angle are 3 degrees and the total range calculated is 67 degrees?
a) 73°
b) 48°
c) 55°
d) 61°
View Answer
Explanation: Given, Λ = 67°, ⌈ = Ω = 3°
Total range angle = powered flight range angle + free-flight range angle + re-entry range angle
Λ = ⌈ + ψ + Ω
67° = 3° + ψ + 3°
ψ = 61°
4. If the ratio of current speed to the local circular speed is 1.58 then which of the orbits is followed by the missile?
a) Circular
b) Elliptical
c) Parabolic
d) Hyperbolic
View Answer
Explanation: The Non-dimensional parameter Q is given by: Q ≡ \(\Big(\frac{v}{v_{cs}}\Big)^2\) = 1.582 ≅ 2.5
Since Q > 2, the missile follows the hyperbolic orbit.
5. If the free flight range angle is given as 90 deg and the non-dimensional parameter at the burn out is 0.9, then what is the value of the high-trajectory flight path angle?
a) 11.1 deg
b) 37.5 deg
c) 4.3 deg
d) 10.5 deg
View Answer
Explanation: Given, ψ = 90°, Qbo = 0.9
The flight path angle is given by:
sin\(\Big(\)2Φbo + \(\frac{\psi}{2}\big) = \frac{2-Q_{bo}}{Q_{bo}}\) sin \(\frac{\psi}{2}\)
sin\(\Big(\)2Φbo + \(\frac{90}{2}\Big) = \frac{2-0.9}{0.9}\) sin \(\frac{90}{2}\)
sin(2Φbo + 47) = 0.8642 ≅ 0.866
2Φbo + 47 = sin-1 0.866
There are two angles with the appropriate sine 60° and 120° thus, there are two values of the flight-path angle:
Φbo = 7.5deg and 37.5 deg
The higher value of flight-path angle corresponds to the high-trajectory.
6. The negative value of flight path angle is practical for carrying out ballistic missile trajectories.
a) True
b) False
View Answer
Explanation: The negative value of flight path angle is achieved when Qbo > 1. In this case there is one positive and one negative value of Φbo. The negative value is impractical as the orbit stays within the Earth.
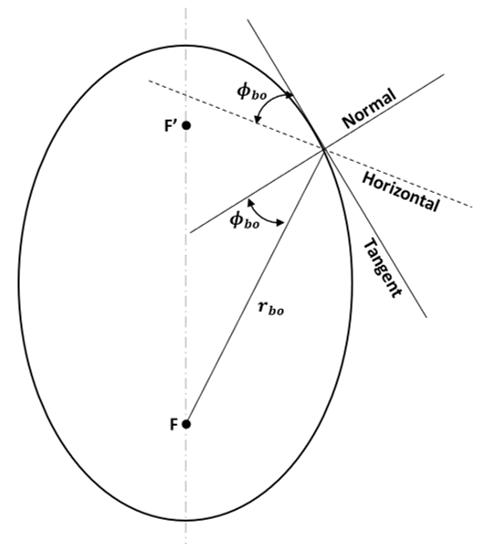
7. Which of these forms the flight-path angle?
a) Angle between the local horizontal and the tangent
b) Angle between the local horizontal and the normal
c) Angle between the normal and the tangent
d) Angle between the velocity at burn-out vector and focal vector
View Answer
Explanation: From the figure shown, the angle between the local horizontal and the tangent (direction of vbo) is the flight-path angle. rbo is perpendicular to the local horizontal and the normal is perpendicular to the tangent, the angle between rbo and the normal is Φbo.
8. Both high and low trajectories have same energy.
a) True
b) False
View Answer
Explanation: Since both the high and low trajectories result from the same rbo and vbo, they both have the same energy. Because a = –\(\frac{\mu}{2\varepsilon}\) and the major axis of the high and low trajectories are of the same length.
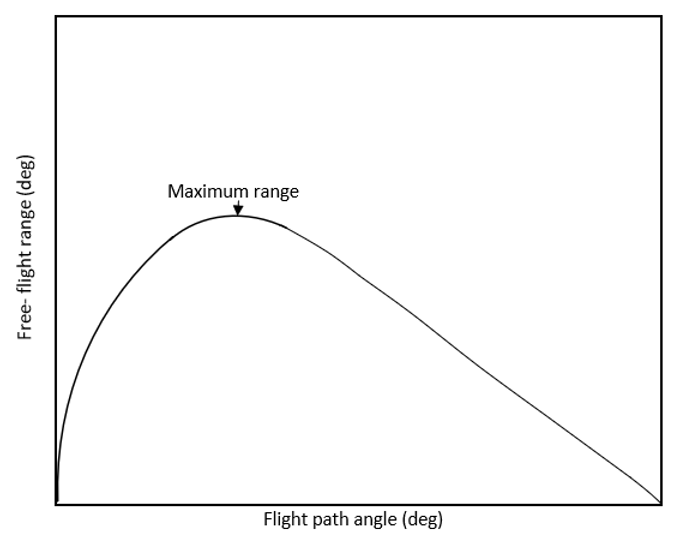
9. At maximum range, how many paths are available to reach the target?
a) 0
b) 1
c) 2
d) 3
View Answer
Explanation: On plotting free flight range vs flight path angle graph, we get a curve as shown in the figure. The flight path angle first increases then decreases within the range of 0-90 degrees. On reaching the maximum point, there’ only one corresponding flight path angle. For rest of the range values, there are two corresponding flight path angles. Thus, there’s is only one path to the target.
10. What is the maximum range angle attained by the missile for the non-dimensional parameter at burn out of 0.79?
a) 81.52 degrees
b) 90.52 degrees
c) 45.14 degrees
d) 40.76 degrees
View Answer
Explanation: Given, Qbo = 0.79
For the maximum range condition, the maximum range angle is computed by:
sin \(\frac{\psi}{2} = \frac{Q_{bo}}{2-Q_{bo}}\)
sin \(\frac{\psi}{2}\) = \(\frac{0.79}{2-0.79}\)
\(\frac{\psi}{2}\) = sin-1 0.653
ψ = 81.52 degrees.
Sanfoundry Global Education & Learning Series – Spaceflight Mechanics.
To practice all areas of Spaceflight Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
