This set of Orbital Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Circular Orbits – Set 2”.
1. How much is the delta-v required to put a satellite in circular orbit of altitude 3,000 km over Mars surface. The satellite is travelling initially at 27 km/s. Radius and gravitational parameter of Mars are 3,389.5 km and 42,828 km3/s2.
a) 24.41 km/s
b) 21.11 km/s
c) 15.8 km/s
d) 22.67 km/s
View Answer
Explanation: Given,
Initial velocity (vi) = 27 km/s
Gravitational Parameter (μ) = 42,828 km3/s2
Radius of Satellite (r) = 3,389.5 + 3,000
= 6,389.5 km
Orbit velocity (v) = (μ/r)1/2
= (42,828/6,389.5)1/2
= 2.589 km/s
Delta-v = vi – v
= 27 – 2.589
= 24.41 km/s
2. What is the escape velocity of a satellite around Venus if its specific angular momentum is 47,862.73 km2/s? The orbit of satellite is circular and gravitational parameter of Venus is 324,859 km3/s2.
a) 10.36 km/s
b) 11.11 km/s
c) 9.599 km/s
d) 9.45 km/s
View Answer
Explanation: Given,
Specific angular momentum (h) = 47,862.73 km2/s
Gravitational parameter (μ) = 324,859 km3/s2
Escape velocity (vesc) = 21/2(μ/h)
= 21/2*(324,859/47,862.73)
= 9.599 km/s
3. What is the time period of revolution of a satellite around Venus if its specific angular momentum is 18,919 mi2/s. The orbit of the satellite is circular. Gravitational parameter of Venus is 77,937.75 mi3/s.
a) 1.809 hours
b) 1.946 hours
c) 2.01 hours
d) 22 hours
View Answer
Explanation: Given,
Specific angular momentum (h) = 18,919 mi2/s
= 18,919 x 1.609342 km2/s
= 49,000 km2/s
Gravitational parameter (μ) = 77,937.75 mi3/s
= 77,937.75 x 1.609343 km3/s
= 324,856 km3/s
Satellite radius (r) = h2/μ
= 49,0002/324,856
= 7,390.967 km
Time period (T) = 2πr3/2μ-1/2
= 2π*7,390.9673/2*324,856-1/2
= 7,004.65 s
= 1.9457 hours
4. Velocity of a satellite in a circular orbit is dependent on radius of orbit, mass of the earth and true anomaly.
a) True
b) False
View Answer
Explanation: False, because the velocity of a satellite in a circular orbit is independent of true anomaly. Unlike, elliptical, parabolic, hyperbolic trajectories where the velocity is dependent on the true anomaly. Mass of the earth/planet and radius of orbit are dependent on the velocity for all cases of orbits.
5. Velocity of a satellite in circular orbit is _____________________ the radius of orbit.
a) directly proportional to
b) inversely proportional to
c) inversely proportional to square root of
d) inversely proportional to square of
View Answer
Explanation: Only for circular orbits is the velocity of a satellite inversely proportional to square root of the radius of orbit. In all the other cases, the relationship is not as straightforward due to the tangential and radial velocity components. It cannot be inversely proportional either, though v = h/r. Since h, is dependent on r. Only equation that best describes the relationship is v = (μ/r)1/2 and μ is a constant.
6. What is the specific energy of an asteroid in a circular orbit around the Sun of radius 4.8 AU. The gravitational parameter of Sun is 1.327124 x 1011 km3/s2.
a) -2.705 m2/s2
b) 92.405 km2/s2
c) -2.705 x 10-3 m2/s2
d) -2.705 x 10-3 km2/s2
View Answer
Explanation: Given,
Radius of orbit (r) = 4.8 AU
= 4.8 x 1.496 x 108 km
= 7.181 x 108 km
Gravitational parameter (μ) = 1.327124 x 1011 km3/s2
Specific energy (ε) = -μ/(2r)
= -(1.327124 x 1011)/(2 x 7.181 x 108)
= 92.405 km2/s2
7. Describe the equation of the circular orbit in cartesian coordinates. Given, a point is P(6,054.78,6492.95) along the orbit in cartesian coordinates. Assume the centre of larger body to be the origin O(0,0).
a) (x – 6,054.78)2 + (y – 6,492.95)2 – 8,878 = 0
b) x2 + y2 – 12,548 = 0
c) x2 + y2 – 8,878 = 0
d) x2 + y2 – 78,818,884 = 0
View Answer
Explanation: Given, origin O(0,0) at larger body centre.
Therefore, point P(6,054.78,6492.95) can be used to determine the orbit radius.
Orbit radius (r) = (6,054.782 + 6492.952)1/2
= 8,878 km
Equation of a circle can be written as x2 + y2 = r2, if origin point is (0,0)
Therefore, equation of circle is
x2 + y2 – 78,818,884 = 0
8. A satellite is in an orbit with a velocity of 3.156 km/s, radius of 3,000 km and eccentricity of 0. What is the specific angular momentum of the satellite?
a) 126,269.5 km2/s
b) 16,269.4 km2/s
c) 9,468 km2/s
d) 14,121.4 km2/s
View Answer
Explanation: For eccentricity e = 0,
Satellite velocity (v) = Tangential velocity = 3.156 km/s
Satellite radius (r) = 3,000 km
Specific angular momentum (h) = rv
= 3,000*3.156
= 9,468 km2/s
9. What is the percentage of visible surface area (shaded area) from the GEO satellite as shown? The surface area can be calculated as (surface area of hemisphere) x (1 – cos(latitude angle)).
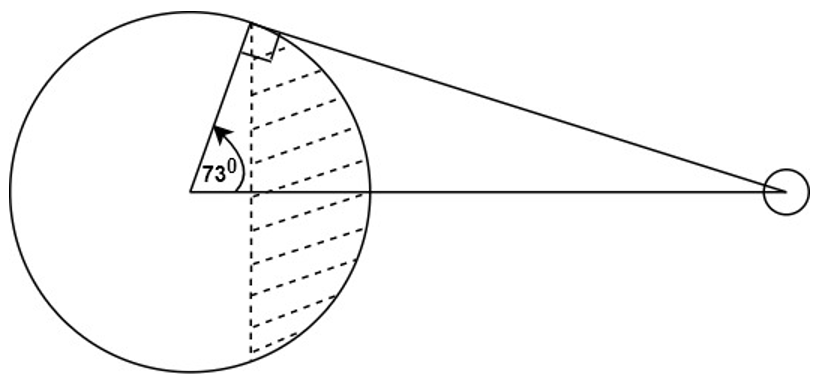
a) 100%
b) 70.76%
c) 69.42%
d) 42.04%
View Answer
Explanation: Given,
Latitude angle (Φ) = 73°
Percentage of visible surface = (Visible surface area) / (Surface area of hemisphere) x 100%
= (Surface area of hemisphere x (1 – cos Φ)) / (Surface area of hemisphere)
x 100%
= (1 – cos Φ) x 100%
= (1 – cos 73°) x 100%
= 70.76%
10. What is the specific energy of a LEO satellite of specific angular momentum of 10,000 km2/s?
a) -149.21 km2/s2
b) -912.01 km2/s2
c) -794.41 km2/s2
d) -49.25 km2/s2
View Answer
Explanation: Given,
The satellite is orbiting Earth, therefore,
Gravitational parameter (μ) = 398,600 km3/s2
Specific angular momentum (h) = 10,000 km2/s
Also, Low Earth Orbits (LEO) are circular, therefore
Specific energy (ε) = -(1/2)(μ/h)2
= -(1/2)(398,600/10,000)2
= -794.41 km2/s2
Sanfoundry Global Education & Learning Series – Orbital Mechanics.
To practice all areas of Orbital Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
