This set of Spaceflight Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “ECI Coordinate System”.
1. Where is the origin of Earth-centered inertial coordinate system situated?
a) At the center of gravity of an aircraft/spacecraft
b) At the fixed point on the Earth’s surface
c) Center of mass of the Earth
d) Center of the mass of the Sun
View Answer
Explanation: The origin of ECI system is located at the mass center of the earth but does not rotate with the Earth. Thus, this is fixed with the relative stars and is hence inertial.
2. In which direction does the X-axis of the ECI system point?
a) Perihelion
b) Vernal equinox
c) Local horizon
d) Along the intersection of Earth’s equatorial plane and the plane of ecliptic
View Answer
Explanation: The X-axis of the ECI system points towards the vernal equinox. Vernal equinox marks the first day of the spring in the northern hemisphere (21 March). It is the line joining the Earth and the sun when the sun passes through earth’s equatorial plane.
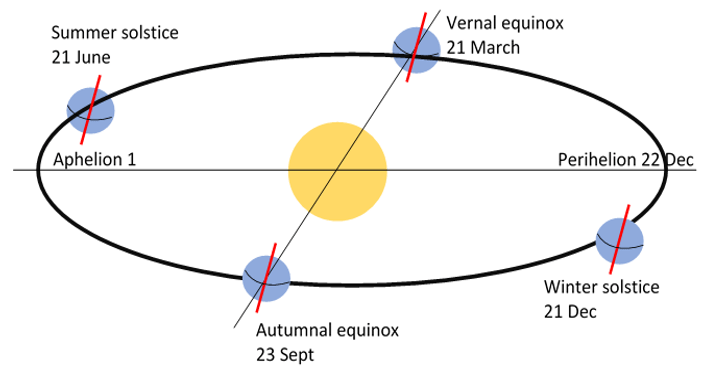
3. In which direction does the Y-axis of ECI system point to?
a) Vernal equinox
b) Points 90 degrees to the west of the x-axis in equatorial plane
c) Normal to the equatorial plane
d) Points 90 degrees to the east of the X-axis in equatorial plane
View Answer
Explanation: The Y-axis of the ECI system points to 90 degrees to the east of the X-axis in the equatorial plane. Y satisfies the cross product of Z and X thus completing the right-handed coordinate system.
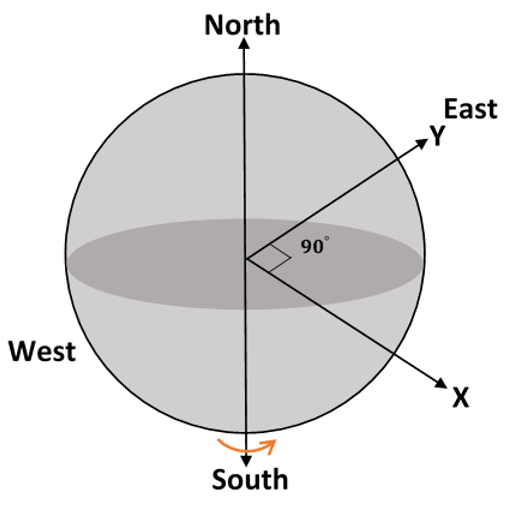
4. What is the relation used to find the right ascension α and declination δ in a non-rotating geo-centric equatorial frame?
a) ûr = cos δ cos α \(\hat I\) + cos δ sin α \(\hat J\) + sin δ \(\hat K\)
b) ûr = cos δ cos α \(\hat I\) + cos δ sin α \(\hat J\) + cos δ \(\hat K\)
c) ûr = cos δ cos α \(\hat I\) – cos δ sin α \(\hat J\) + sin δ \(\hat K\)
d) ûr = cos δ cos α \(\hat I\) – cos δ sin α \(\hat J\) + cos δ \(\hat K\)
View Answer
Explanation: If there is a satellite/an object present in the space, the projection of the object on X-axis will be given by:
cos δ cos α
Where cos δ first projects it along the dashed line as shown, and further projection of this vector using cos α ultimately projects it on the X-axis.
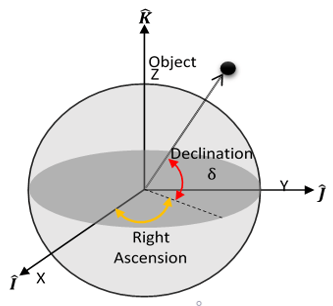
Similarly, projection of the object on Y-axis will be given by:
cos δ sin α
And projection of the object on Z-axis will be given by:
sin δ
On addition of these individual vector projections, we arrive at ûr = cos δ cos α \(\hat I\) + cos δ sin α \(\hat J\) + sin δ \(\hat K\).
5. What is the angle of declination if the position vector of the satellite is \(\vec r\) = -5000 \(\hat I\) + 2000 \(\hat J\) + 4000 \(\hat K\) (km) ?
a) 53.41°
b) 88.92°
c) 36.73°
d) 65.12°
View Answer
Explanation: The magnitude of the vector of the form \(\vec x\) = A\(\hat I\) + B\(\hat J\) + C\(\hat K\) is given by:
x = \(\sqrt{(A)^2 + (B)^2 + (C)^2}\)
Magnitude of \(\vec r\) is:
r = \(\sqrt{(-5000)^2 + (2000)^2 + (4000)^2}\) = 6708.2 km
\(\hat u_r\) = \(\frac{\vec r}{r} = \frac{-5000}{6708.2} \hat I + \frac{2000}{6708.2} \hat J + \frac{4000}{6708.2} \hat K\)
\(\hat u_r\) = -0.745\(\hat I\) + 0.298\(\hat J\) + 0.596\(\hat K\)
Since \(\hat u_r\) = cos δ cos α \(\hat I\) + cos δ sin α \(\hat J\) + sin δ \(\hat K\), on comparison we get
sin δ \(\hat K\) = 0.596\(\hat K\)
δ = sin-10.598 = 36.73°
6. What is the angle of ascension if the position vector of the satellite launched by NASA is \(\vec r\) = 2500 \(\hat I\) + 1900 \(\hat K\) (km) ?
a) 1.3585°
b) 2.9489°
c) 16.14°
d) 1.2148°
View Answer
Explanation: The magnitude of the vector of the form \(\vec x\) = A\(\hat I\) + B\(\hat J\) + C\(\hat K\) is given by:
x = \(\sqrt{(A)^2 + (B)^2 + (C)^2}\)
Magnitude of \(\vec r\) is:
r = \(\sqrt{(2500)^2 + (1900)^2}\) = 3140 km
\(\hat u_r\) = \(\frac{\vec r}{r} = \frac{2500}{3140} \hat I + \frac{1900}{3140}\hat K\)
\(\hat u_r\) = 0.796 \(\hat I\) + 0.605 \(\hat K\)
Since \(\hat u_r\) = cos δ cos α \(\hat I\) + cos δ sin α \(\hat J\) + sin δ \(\hat K\), on comparison we get
sin δ \(\hat K\) = 0.605 \(\hat K\)
δ = sin-1 (0.605) = 37.229°
cosδ cosα \(\hat I\) = 0.796 \(\hat I\)
cosα = \(\frac{0.796}{cos \,37.229^°}\) = 0.9997
α = cos-1 0.9997 = 1.3585°
7. What angle is formed between the Earth’s equatorial plane and ecliptic plane?
a) 25°
b) 21.5°
c) 23.4°
d) 22°
View Answer
Explanation: The angle formed between the Earth’s ecliptic plane/orbit plane and the equatorial plane is 23.4°. This is because of the fact that Earth does not rotate perpendicularly in the orbital plane and is therefore inclined.
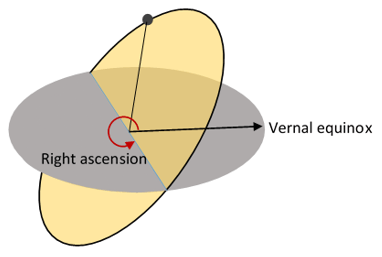
8. What is the angle of the right ascension?
a) Angle between vernal equinox and ascending node on equatorial plane
b) Angle between ascending node and perigee
c) Angle between the orbital and equatorial plane
d) Angle between the perigee and satellite in orbital plane
View Answer
Explanation: Right ascension is the angle formed between the vernal equinox vector to the ascending node on the equatorial plane. Angle between ascending node and perigee is known as Argument of perigee, angle between the orbital and equatorial plane is called Inclination and finally the perigee and satellite in orbital plane’s angle is known as True anomaly.
Sanfoundry Global Education & Learning Series – Spaceflight Mechanics.
To practice all areas of Spaceflight Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
