This set of Spaceflight Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Attitude and Kinematics of Coordinate Frames”.
1. What parameter changes after coordinate transformation?
a) Angular rotation
b) Length
c) Direction
d) Magnitude
View Answer
Explanation: The coordinate transformation changes only the basis of vector, the rest i.e. length and direction after coordinate transformation remains the same.
2. If a point having coordinates (x,y) has to be reflected across line y = x, then what will be the coordinates of the reflected point?
a) (x, -y)
b) (-x, -y)
c) (x, y)
d) (-x, y)
View Answer
Explanation: When a point has to be reflected across the y-axis, the y value stays the same and the x value becomes opposite of what it is.
3. Orthogonal axes XYZ having position vector \(\vec{r}_{XYZ}\) is rotated by an angular rotation of χ about Z-axis resulting in X’Y’Z’ coordinate system, then what is the new position vector?
a) \(\vec{r}_{X’Y’Z’}\) = \(\begin{bmatrix}-cosχ & -sinχ & 0 \\-sinχ & -cosχ & 0 \\0 & 0 & 1 \end {bmatrix}\) \(\vec{r}_{XYZ}\)
b) \(\vec{r}_{X’Y’Z’}\) = \(\begin{bmatrix}cosχ & sinχ & 0 \\-sinχ & cosχ & 0 \\0 & 0 & 1 \end {bmatrix}\) \(\vec{r}_{XYZ}\)
c) \(\vec{r}_{X’Y’Z’}\) = \(\begin{bmatrix}-cosχ & -sinχ & 0 \\sinχ & -cosχ & 0 \\0 & 0 & 1 \end {bmatrix}\) \(\vec{r}_{XYZ}\)
d) \(\vec{r}_{X’Y’Z’}\) = \(\begin{bmatrix}sinχ & cosχ & 0 \\cosχ & sinχ & 0 \\0 & 0 & 1 \end {bmatrix}\) \(\vec{r}_{XYZ}\)
View Answer
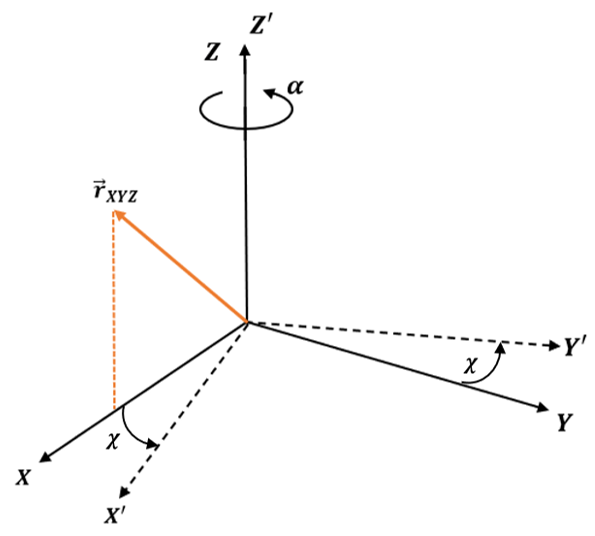
Explanation: In the figure below, it shows the rotation of orthogonal axes XYZ into X’Y’Z’ by rotating it through angle χ about Z axis. The Z’ is aligned with the original Z axis only. X and Y axis stay in the same plane which are rotated by angle χ to form X’ and Y’ respectively. The new position vector thus resulting is:
\(\vec{r}_{X’Y’Z’}\) = \(\begin{bmatrix}cosχ & sinχ & 0 \\-sinχ & cosχ & 0 \\0 & 0 & 1 \end {bmatrix}\) \(\vec{r}_{XYZ}\)
By carrying out matrix multiplication, we will obtain the new position vector. The Z components of both \(\vec{r}_{XYZ}\) and \(\vec{r}_{X’Y’Z’}\) are same because the Z-components remain same before and after rotation. 1 in the lower right corner of the matrix preserves the Z-components.
4. If the position vector if the point in XYZ axis is \(\vec{r}_{XYZ}\) = 8I + 4J – 2K, then what will be the new position vector if there is a simple rotational transformation of +25 deg about Z-axis resulting in X’Y’Z’ axis?
a) \(\vec{r}_{X’Y’Z’}\) = 0.244I + 8.94J
b) \(\vec{r}_{X’Y’Z’}\) = 2.41I + 0.542J + 2K
c) \(\vec{r}_{X’Y’Z’}\) = 10.945I – 2J + 0.241K
d) \(\vec{r}_{X’Y’Z’}\) = 8.94I + 0.244J – 2K
View Answer
Explanation: Given, \(\vec{r}_{XYZ}\) = 8I + 4J – 2K, α = 25°
The new position vector upon rotating the coordinate frame by an angle about Z-axis is:
\(\vec{r}_{X’Y’Z’}\) = \(\begin{bmatrix}cos\alpha & sin\alpha & 0 \\-sin\alpha & cos\alpha & 0 \\0 & 0 & 1 \end {bmatrix}\) \(\vec{r}_{XYZ}\)
Substituting the values:
\(\vec{r}_{X’Y’Z’}\) = \(\begin{bmatrix}cos25 & sin25 & 0 \\-sin25 & cos25 & 0 \\0 & 0 & 1 \end {bmatrix}\) \(\begin{bmatrix}8 \\4 \\-2 \end {bmatrix}\)
\(\vec{r}_{X’Y’Z’}\) = (8cos25 + 4sin25 – 0)I + (-8sin25 + 4cos25 – 0)J + (0 + 0 – 2)K
\(\vec{r}_{X’Y’Z’}\) = 8.94I + 0.244J – 2K
5. The rotational matrix used for coordinate transformation is which kind of matrix?
a) Orthogonal matrix
b) Skew matrix
c) Identical matrix
d) Rotational matrix
View Answer
Explanation: The rotational matrix associated with the positive rotation about Z-axis is given by:
C(α) = \(\begin{bmatrix}cos\alpha & sin\alpha & 0 \\-sin\alpha & cos\alpha & 0 \\0 & 0 & 1 \end {bmatrix}\)
This matrix is orthogonal matrix i.e. it’s rows and columns are orthogonal unit vectors. The dot product of any two rows or columns is zero.
6. Orthogonal axes XYZ having position vector \(\vec{r}_{XYZ}\) is rotated by an angular rotation of α about X-axis resulting in X’Y’Z’ coordinate system, then what is the new position vector?
a) \(\vec{r}_{X’Y’Z’}\) = \(\begin{bmatrix}1 & 0 & 0 \\0 & cos\alpha & sin\alpha \\0 & -sin\alpha & cos\alpha \end {bmatrix}\)\(\vec{r}_{XYZ}\)
b) \(\vec{r}_{X’Y’Z’}\) = \(\begin{bmatrix}cos\alpha & sin\alpha & 0 \\-sin\alpha & cos\alpha & 0 \\0 & 0 & 1 \end {bmatrix}\)\(\vec{r}_{XYZ}\)
c) \(\vec{r}_{X’Y’Z’}\) = \(\begin{bmatrix}-cos\alpha & -sin\alpha & 0 \\0 & 1 & 0 \\-sin\alpha & cos\alpha & 1 \end {bmatrix}\)\(\vec{r}_{XYZ}\)
d) \(\vec{r}_{X’Y’Z’}\) = \(\begin{bmatrix}cos\alpha & -sin\alpha & 0 \\cos\alpha & sin\alpha & 0 \\0 & 0 & 1 \end {bmatrix}\)\(\vec{r}_{XYZ}\)
View Answer
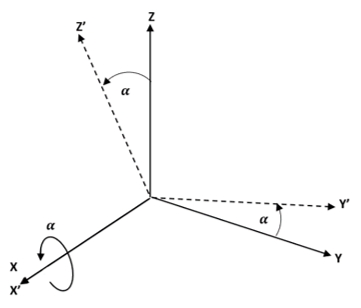
Explanation: In the figure below, it shows the rotation of orthogonal axes XYZ into X’Y’Z’ by rotating it through angle α about X axis. The X’ is aligned with the original X axis only. Z and Y axis stay in the same plane which are rotated by angle α to form Z’ and Y’ respectively. The new position vector thus resulting is:
\(\vec{r}_{X’Y’Z’}\) = \(\begin{bmatrix}1 & 0 & 0 \\0 & cos\alpha & sin\alpha \\0 & -sin\alpha & cos\alpha \end {bmatrix}\)\(\vec{r}_{XYZ}\)
By carrying out matrix multiplication, we will obtain the new position vector. The X components of both \(\vec{r}_{XYZ}\) and \(\vec{r}_{X’Y’Z’}\) are same because the X-components remain same before and after rotation. 1 in the upper left corner of the matrix preserves the X-components.
7. What is the rotational matrix if the rotation of cartesian XYZ frame takes place about Y axis?
a) \(\begin{bmatrix}1 & 0 & 0 \\0 & cos\beta & sin\beta \\0 & -sin\beta & cos\beta \end {bmatrix}\)
b) \(\begin{bmatrix}cos\alpha & sin\alpha & 0 \\-sin\alpha & cos\alpha & 0 \\0 & 0 & 1\end {bmatrix}\)
c) \(\begin{bmatrix}cos\beta & 0 & -sin\beta \\0 & 1 & 0 \\sin\beta & 0 & cos\beta \end {bmatrix}\)
d) \(\begin{bmatrix}1 & 0 & 0 \\0 & cos\alpha & sin\alpha \\0 & -sin\alpha & cos\alpha \end {bmatrix}\)
View Answer
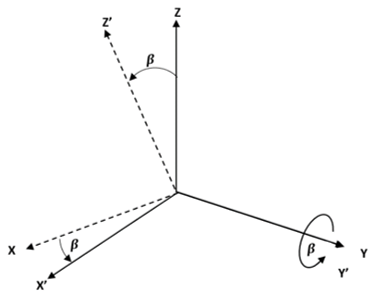
Explanation: The rotation of the cartesian frame XYZ about Y axis through angle β produces X’Y’Z’ frame.
The rotational matric is again orthogonal matrix with 1 in center of the matrix preseving the Y-components of the matrix.
The rotational matrix formed is: \(\begin{bmatrix}cos\alpha & sin\alpha & 0 \\-sin\alpha & cos\alpha & 0 \\0 & 0 & 1\end {bmatrix}\)
8. How many rotations are required to transform the ECI coordinate system to the perifocal system?
a) 0
b) 1
c) 2
d) 3
View Answer
Explanation: The coordinate transformation from XYZ frame to X’Y’Z’ frame is carried out by a single rotation about one axis. The other two axes remain in the same plane. But to transform from the ECI coordinate system to the perifocal system, there have to be successive 3 rotations. The first rotation is about Z axis, second is through X’ axis and the final rotation is bout Z’’ axis.
9. What is the order of rotation to convert the ECI coordinate system to perifocal system?
a) About +Z axis, +X’ axis, +Z’’ axis
b) About +X axis, +Y axis
c) About +Z axis, +Y axis, +X axis
d) About +X axis, +Y axis, +Z axis
View Answer
Explanation: In order to transform from the ECI coordinate system to the perifocal system, there have to be successive 3 rotations. The first rotation is about Z axis through the ascending node Ω. The second rotation is through X’ axis through inclination i, and the final rotation is bout Z’’ axis through argument of perigee ω.
\(\vec{r}_{ECI}\) = [C(ω) A(i) C(Ω)]-1\(\vec{r}_{PQW}\)
10. What is the rotational matrix to carry out coordinate transformation from perifocal system to ECI coordinate system?
a) \(\tilde{R} = \begin{bmatrix}s_\omega s_i & -c_\omega s_i & c_i \\s_\Omega c_\omega + c_\Omega s_\omega c_i & -s_\Omega s_\omega + c_\Omega c_\omega c_i & -c_\Omega s_i \\c_\Omega c_\omega – s_\Omega s_\omega c_i & c_\Omega s_\omega – s_\Omega c_\omega c_i & s_\Omega s_i \end {bmatrix}\)
b) \(\tilde{R} = \begin{bmatrix}c_\Omega c_\omega + s_\Omega s_\omega c_i & -c_\Omega s_\omega + s_\Omega c_\omega c_i & -s_\Omega s_i \\s_\Omega c_\omega + c_\Omega s_\omega c_i & -s_\Omega s_\omega + c_\Omega c_\omega c_i & -c_\Omega s_i \\-s_\omega s_i & -c_\omega s_i & -c_i \end {bmatrix}\)
c) \(\tilde{R} = \begin{bmatrix}c_\Omega c_\omega – s_\Omega s_\omega c_i & -c_\Omega s_\omega – s_\Omega c_\omega c_i & s_\Omega s_i \\s_\omega s_i & c_\omega s_i & -c_i \\s_\Omega c_\omega + c_\Omega s_\omega c_i & -s_\Omega s_\omega + c_\Omega c_\omega c_i & c_\Omega s_i \end {bmatrix}\)
d) \(\tilde{R} = \begin{bmatrix}c_\Omega c_\omega – s_\Omega s_\omega c_i & -c_\Omega s_\omega – s_\Omega c_\omega c_i & s_\Omega s_i \\s_\Omega c_\omega + c_\Omega s_\omega c_i & -s_\Omega s_\omega + c_\Omega c_\omega c_i & -c_\Omega s_i \\s_\omega s_i & c_\omega s_i & c_i \end {bmatrix}\)
View Answer
Explanation: The inverse of matrix C(ω) A(i) C(Ω) gives us the rotational matrix \(\tilde{R}\) that transforms the vector from perifocal frame to ECI coordinate frame. Each of the matrix is orthogonal, thus the product of these three matrices also results in an orthogonal matrix.
Rotation matrix is given as:
\(\tilde{R} = \Bigg[\begin{bmatrix}cos\omega & sin\omega & 0 \\-sin\omega & cos\omega & 0 \\0 & 0 & 1\end {bmatrix} \begin{bmatrix}1 & 0 & 0 \\0 & cosi & sini \\0 & -sini & cosi \end {bmatrix} \begin{bmatrix}cos\Omega & sin\Omega & 0 \\-sin\Omega & cos\Omega & 0 \\0 & 0 & 1\end {bmatrix} \Bigg]^T\)
This results in:
\(\tilde{R} = \begin{bmatrix}c_\Omega c_\omega – s_\Omega s_\omega c_i & -c_\Omega s_\omega – s_\Omega c_\omega c_i & s_\Omega s_i \\s_\Omega c_\omega + c_\Omega s_\omega c_i & -s_\Omega s_\omega + c_\Omega c_\omega c_i & -c_\Omega s_i \\s_\omega s_i & c_\omega s_i & c_i \end {bmatrix}\) Where cΩ is cosΩ, cω is cosω and ci is cosi
Same is for sΩ, sω and si
Sanfoundry Global Education & Learning Series – Spaceflight Mechanics.
To practice all areas of Spaceflight Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
