This set of Orbital Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Bi-Elliptical Transfer”.
1. How many orbital maneuvers are carried out in Bi-Elliptical transfer?
a) 0
b) 1
c) 2
d) 3
View Answer
Explanation: There are three orbital maneuvers carried out in a bi-elliptical orbit. The first maneuver moves spacecraft into an elliptical transfer orbit, second maneuver raises periapsis of first transfer ellipse equal to radius of outer circle. The final maneuver reduces the radius at apogee of the second transfer ellipse to equal the radius of the outer circle.
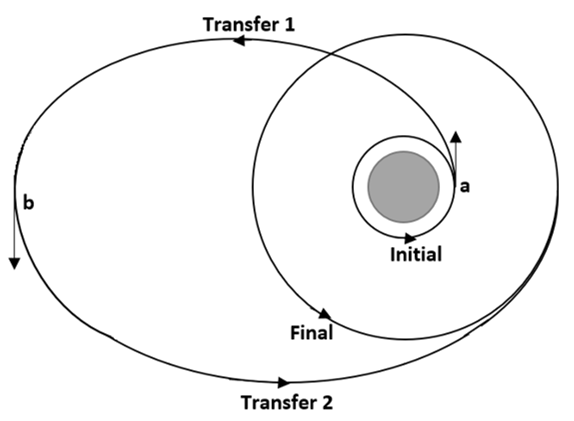
2. How many impulses are given in Bi-elliptic maneuver to move the object from 2st orbit to the second?
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: In the bi-elliptic orbit, there are two delta-v burn provided. The first burn is at the apogee of the initial circular orbit whichmakes it enter into first transfer orbit. After this, the second burn is at the perigee of the transfer orbit 1 which makes the object enter the second transfer orbit.
3. Bi-elliptic maneuver requires more delta-v than the Hohmann transfer due to more impulses applied.
a) True
b) False
View Answer
Explanation: Despite making use of more than one engine burn, bi-elliptic maneuver is more efficient than the Hohmann transfer. It has a greater travel time, but requires less delta-v in total.
4. In which orbit does the object enter after first orbital maneuver in bi-elliptic transfer?
a) First transfer orbit
b) Second transfer orbit
c) Parking orbit
d) Final orbit
View Answer
Explanation: In the first maneuver of the bi-elliptic transfer, the object is moves to the first transfer ellipse that has a radius much larger than the radius of the final circular orbit.
5. In which orbit does the object enter after second orbital maneuver in bi-elliptic transfer?
a) First transfer orbit
b) Second transfer orbit
c) Parking orbit
d) Final orbit
View Answer
Explanation: In the first maneuver of the bi-elliptic transfer, the object is moves to the second transfer ellipse. This raises the perigee of the first transfer ellipse equal to the radius of the outer circle.
6. The radius of the elliptical orbit in bi-elliptical hohmann transfer is a free entity.
a) True
b) False
View Answer
Explanation: r* is a free parameter and can have any value. Usually as r* tends to infinity, the bi-elliptic tranfer becomes more efficient. As r* tends to infinity, time tends to infinity so there is trade-off between time and efficiency.
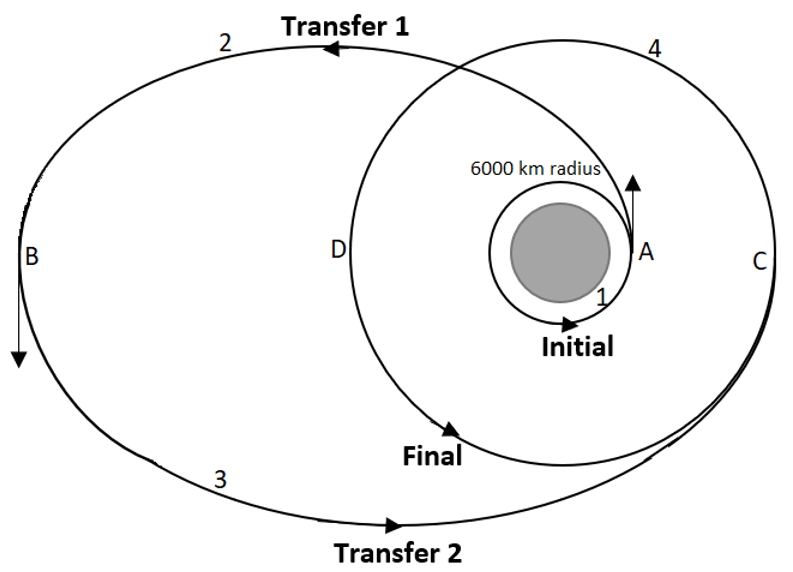
7. What is the total delta-v required for bi-elliptic transferfrom a geocentric circular orbit of 6000 km radius to 98,000 km radius? (Given- apogee of first ellipse is 120,000 km).
a) 0.0145 km/s
b) 2.145 km/s
c) 3.245 km/s
d) 4.759 km/s
View Answer
Explanation: rA = 6,000 km, rB = 98,000 km, rC = rD = 120,000 km
For orbit 1: It is a circular orbit
vA1 = \(\sqrt{\frac{\mu}{r_A}} = \sqrt{\frac{398,600}{6,000}}\) = 8.15 km/s
For orbit 2: It is a transfer ellipse orbit
h2 = \(\sqrt{2\mu} \sqrt{\frac{r_A r_B}{r_A + r_B}} = \sqrt{2 × 398,600} \sqrt{\frac{6,000 × 98,000}{6,000 + 98,000}}\) = 67,136 km2/s
vA2 = \(\frac{h_2}{r_A} = \frac{67,136}{6,000}\) = 11.189 km/s
vB2 = \(\frac{h_2}{r_B} = \frac{67,136}{98,000}\) = 0.685 km/s
For orbit 3: It is the second transfer ellipse orbit
h3 = \(\sqrt{2\mu} \sqrt{\frac{r_B r_C}{r_B + r_C}} = \sqrt{2 × 398,600} \sqrt{\frac{98,000 × 120,000}{98,000 + 120,000}}\) = 207,376.27 km2/s
vB3 = \(\frac{h_2}{r_B} = \frac{207,376.27}{98,000}\) = 2.116 km/s
vC3 = \(\frac{h_2}{r_C} = \frac{207,376.27}{120,000}\) = 1.728 km/s
For orbit 4: The final orbit
vC4 = vD4 = \(\sqrt{\frac{\mu}{r_C}} = \frac{398,600}{98,000}\) = 2.017 km/s
Δvtotal = ΔvA + ΔvB + ΔvC
Δvtotal |vA2 – vA1| + |vB3 – vB2| + |vC4 – vC3|
Δvtotal |11.189 – 8.15 | + |2.116 – 0.685| + |2.017 – 1.728| = 4.759 km/s
8. Which of these orbital transfers is the most energy efficient?
a) Bi-elliptic transfer
b) One tangent-burn transfer
c) Hohmann transfer
d) Non-Hohmann transfer
View Answer
Explanation: Hohmann transfer is considered at the most energy efficient two-impulse transfer. It does not truly exist. In this, both the initial and final orbital planes are coplanar and the change in velocity magnitude is tangential to both the initial and final orbits.
9. What is the time-period of the bi-elliptic transfer if the semi-ellipses of both the transfers are 100,000 km and 120,000 km respectively?
a) 2.12 days
b) 4.22 days
c) 5.10 days
d) 6.14 days
View Answer
Explanation: Given: a2 = 100,000 km, a3 = 120,000 km
The time of flight for the bi-elliptic transfer is given by:
tBi-elliptic = \(\frac{1}{2} \Big(\frac{2\pi }{\sqrt \mu} a_2^{\frac{3}{2}} + \frac{2\pi }{\sqrt \mu} a_2^{\frac{3}{2}}\Big)\)
tBi-elliptic = \(\frac{1}{2} \Big(\frac{2\pi}{\sqrt {398,600}}\) 100,0003/2 + \(\frac{2\pi }{\sqrt {398,600}}\) 120,0003/2\(\Big) \)
tBi-elliptic = \(\frac{1}{2}\) (314710.4915 + 41369.6846) = 364,204.0881 s = 4.22 days.
10. Which of these burns is retrograde in bi-elliptic transfer?
a) First burn
b) Second burn
c) Third burn
d) Fourth burn
View Answer
Explanation: The third burn is retrograde i.e. the burn is opposite to the direction of the motion. This is done to slow down the object and circularize the orbit by lowering the perigee to the final orbit’s radius.
Sanfoundry Global Education & Learning Series – Orbital Mechanics.
To practice all areas of Orbital Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
