This set of Spaceflight Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Ballistic Missiles Trajectories – Earth’s Rotation Effect”.
1. What is the surface velocity at the equator due to Earth’s rotation?
a) 1000 ft/s
b) 1524 ft/s
c) 2834 ft/s
d) 3102 ft/s
View Answer
Explanation: The Earth rotates once on its axis in 23 hours 56 min producing a surface velocity at the equator of 1524 ft/sec. The rotation is from west to east.
2. Both the launch point and target of the ballistic missile trajectory are in motion relative to the inertial frame.
a) True
b) False
View Answer
Explanation: The free-flight portion of a ballistic missile trajectory is inertial in character. That is, it remains fixed in the XYZ inertial frame while the earth runs under it. Relative to this inertial XYZ frame, both the launch point and the target are in motion.
3. How is the initial velocity of the ballistic missile compensated?
a) Adding the initial eastward velocity of launch site
b) Subtracting the initial eastward velocity of launch site
c) Adding the initial westward velocity of launch site
d) Subtracting the initial westward velocity of launch site
View Answer
Explanation: The compensation for the initial velocity is done by recognizing that the true velocity of the missile at burnout is the velocity relative to the launch site (which could be measured by radar) plus the initial eastward velocity of the launch site due to earth rotation.
4. What is the formula to compute the speed of any launch point on surface of earth?
a) v0 = cosL0 ft/s
b) v0 = 1524 sinL0 ft/s
c) v0 = 1524 cosL0 ft/s
d) v0 = sinL0 ft/s
View Answer
Explanation: Since a point on the equator has a speed of 1,524 ft/sec (464.52 m/s) in the eastward direction, we can express the speed of any launch point on the surface of the earth as:
v0 = 1524 cosL0 ft/s
Where L0 is the latitude of the launch site.
5. What is the formula for computing the Azimuth angle?
a) tanβ = \(\frac{-V_E}{V_S}\)
b) tanβ = \(\frac{V_E}{V_S}\)
c) tanβ = \(\frac{-V_S}{V_E}\)
d) tanβ = \(\frac{-V_E}{V_N}\)
View Answer
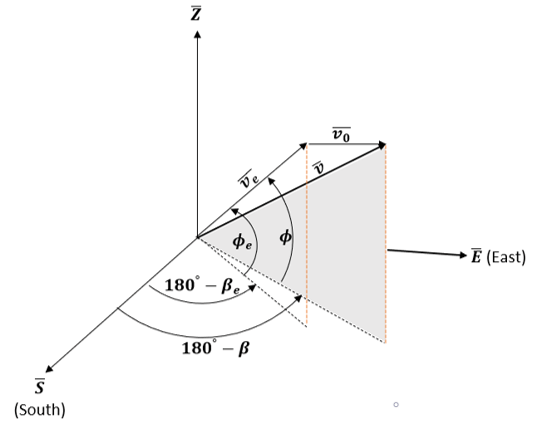
Explanation: Azimuth angle β is measured clockwise from the local north-pointing longitude line at the launch site. This is calculated by breaking true velocity components into itseastward and southward components.
Where, VE = vE cosΦe sinβe + v0
VS = -vE cosΦe cosβe
6. What is the magnitude of true speed of the launch?
a) v = \(\sqrt{v_S^2 + v_E^2 + v_Z^2 + v_W^2}\)
b) v = \(\sqrt{v_S^2 + v_E^2 + v_W^2}\)
c) v = \(\sqrt{v_S^2 + v_E^2}\)
d) v = \(\sqrt{v_S^2 + v_E^2 + v_Z^2}\)
View Answer
Explanation: We can obtain the south, east and up components of the true velocity, v, by breaking up vE into its components and adding v0 to the eastward (E) component. Thus, true speed is given as:
v = \(\sqrt{v_S^2 + v_E^2 + v_Z^2}\)
Where, VE = vE cosΦe sinβe + v0
VS = -vE cosΦe cosβe
VZ = vE sinΦe
7. We cannot compensate for the movement of target due to earth’s rotation.
a) True
b) False
View Answer
Explanation: We compensate for the motion of the target by leading it slightly. If we know the time-of-flight of the missile, we can compute how much the earth (and target) will turn in that time and can aim for a point of actual target. It is a point at the same latitude as the target but east of it an amount equal to the number of degrees the earth will turn during the total time the missile is in flight.
8. What is the formula used to compute the range provided the coordinates of launch point, target and total time of flight is given?
a) cosΛ = sinL0 sinLt + cosL0 cosLt cos(ΔN + ω⊕ tΛ)
b) cosΛ = sinL0 sinLt + cosL0 cosLt
c) sinΛ = sinL0 sinLt + cosL0 cosLt cos(ΔN + ω⊕ tΛ)
d) sinΛ = sinL0 sinLt + cosL0 cosLt
View Answer
Explanation: If we assume that we know the coordinates of the launch point and target and the total time-of-flight tΛ, we can use the law of cosines to obtain:
cosΛ = sinL0 sinLt + cosL0 cosLt cos(ΔN + ω⊕ tΛ)
Where, L0 and N0 are the latitude and longitude coordinates of the launch point.
Lt and Nt are the latitude and longitude coordinates of the target point.
The angular rate, ω⊕ at which the earth turns is approximately 15°/hr.
9. How is the launch azimuth angle calculated?
a) sinΛ = \(\frac{sinL_t-sinL_0 cos\bigwedge}{cosL_0 sin\bigwedge}\)
b) cosβ = \(\frac{sinL_t-sinL_0}{cosL_0}\)
c) cosβ = \(\frac{sinL_t-sinL_0 cos\bigwedge}{cosL_0 sin\bigwedge}\)
d) sinβ = \(\frac{sinL_t-sinL_0 cos\bigwedge}{cosL_0 sin\bigwedge}\)
View Answer
Explanation: The required launch azimuth provided we know the coordinates of the launch point and target and the total time-of-flight is given by:
cosβ = \(\frac{sinL_t-sinL_0 cos\bigwedge}{cosL_0 sin\bigwedge}\)
Where, L0 and N0 are the latitude and longitude coordinates of the launch point.
Lt and Nt are the latitude and longitude coordinates of the target point.
The angular rate, ω⊕ at which the earth turns is approximately 15°/hr.
10. A missile is fired from a station located at (40°N, 125°E) to the target located at (62°N, 150°E). What is the target range if the total flight time is 1000 seconds?
a) 2514.23 km
b) 3135.49 km
c) 4847.50 km
d) 6348.74 km
View Answer
Explanation: Given, L0 = 40°, Lt = 62°, N0 = 125°, Nt = 150°, tΛ = 1000 sec
ΔN = Nt – N0 = 150 – 125 = 25°
ω⊕ = \(\frac{15deg}{hr}\) = 0.00417 deg/sec = 0.00007272 rad/s
cosΛ = sinL0 sinLt + cosL0 cosLt cos(ΔN + ω⊕ tΛ)
Substituting all the values:
cosΛ = sin40 sin62 + cos40 cos62 cos(25 + 0.00417 × 1000)
Range angle = cos-1 0.8815 = 28.16 deg = 0.4916 rad
Range = Radius of Earth × Range angle (in radians)
Range = 6378 × 0.4916 = 3135.49 km.
11. A missile is fired from a station located at (35°N, 100°E) to the target located at (58°N, 109°E). What is the required launch azimuth if the total flight time is 950 seconds?
a) 16.6 deg
b) 21.5 deg
c) 18.7 deg
d) 24.57 deg
View Answer
Explanation: Given, L0 = 35°, Lt = 58°, N0 = 100°, Nt = 109°, tΛ = 950 sec
Launch Azimuth is given by:
cosβ = \(\frac{sinL_t – sinL_0 cos\bigwedge}{cosL_0 sin\bigwedge}\)
But first we need to compute the value of range angle (∧)
ΔN = Nt – N0 = 109 – 100 = 9°
ω⊕ = \(\frac{15deg}{hr}\) = 0.00417 deg/sec = 0.00007272 rad/s
cos∧ = sinL0 sinLt + cosL0 cosLt cos(ΔN + ω⊕ tΛ)
Substituting all the values:
cos∧ = sin35 sin58 + cos35 cos58 cos(9 + 0.00417 × 950)
Range angle = cos-1 0.9094 = 24.57
Substituting the values we will get the launch azimuth:
cosβ = \(\frac{sin58-sin35\, cos24.57}{cos35\, sin24.57}\) = 0.9583
β = cos-1 0.9583 = 16.6 deg.
Sanfoundry Global Education & Learning Series – Spaceflight Mechanics.
To practice all areas of Spaceflight Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
