This set of Orbital Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Two Body Orbital Mechanics”.
1. The solution to a two-body problem is an approximation.
a) True
b) False
View Answer
Explanation: True but the approximation is very close to the actual value and therefore satellites or moons orbiting around the earth are solved as two-body problems. The perturbations due to other celestial bodies for a system like earth and its satellites will be negligible.
2. What is the tangential velocity of a spacecraft around earth. Given, the orbit is circular, and the specific angular momentum of spacecraft is 57,112 km2/s. Standard gravitational parameter of earth is 398,600 km3/s2?
a) 4.99 km/s
b) 5.23 km/s
c) 6.01 km/s
d) 6.98 km/s
View Answer
Explanation: Given,
Standard gravitational parameter (μ) = 398,600 km3/s2
Specific angular momentum (h) = 57,112 km2/s
Eccentricity for a circular orbit (e) = 0
Tangential velocity can then be given by:
vT = (μ/h)(1 + ecosθ)
= (398,600/57,112)(1 + 0)
= 6.98 km/s
3. What is the radial velocity of a spacecraft travelling in a parabolic orbit with a true anomaly of 0.52 rad? Given, the orbit is circular, and the specific angular momentum of spacecraft is 57,112 km2/s. Standard gravitational parameter of earth is 398,600 km3/s2?
a) 3.99 km/s
b) 2.01 km/s
c) 2.19 km/s
d) 3.47 km/s
View Answer
Explanation: Given,
Standard gravitational parameter (μ) = 398,600 km3/s2
Specific angular momentum (h) = 57,112 km2/s
Eccentricity for a parabolic orbit (e) = 1
True anomaly (θ) = 0.52 rad
Radial velocity can then be given by:
vr = (μ/h)(esinθ)
= (398,600/57,112)(1*sin(0.52 rad))
= 3.47 km/s
4. Position vector of a spacecraft is given by point A (1200 km, 0.0059t rad), where t represents time variable. What is the tangential velocity of the spacecraft?
a) 6.23 km/s
b) 7.97 km/s
c) 7.08 km/s
d) 9.01 km/s
View Answer
Explanation: Polar coordinates are represented as (r, θ)
Therefore, r = 1200 km
θ(t) = 0.0059t rad
vT = r(dθ(t)/dt)
= 1200*0.0059
= 7.08 km/s
5. What is the true anomaly of the spacecraft? Given, position vector 2100 i + 1850 j km.
a) 0.88 rad
b) 1.004 rad
c) 0.67 rad
d) 0.73 rad
View Answer
Explanation: Given,
x = 2100 km
y = 1850 km
True anomaly (θ) = atan(y/x)
= atan (1850/2100)
= 0.88 rad
6. What is the flight path angle of spacecraft in an elliptical orbit with eccentricity 0.77 and true anomaly of 37°.
a) 14.15°
b) 16.01°
c) 22.12°
d) 25.02°
View Answer
Explanation: Given,
Eccentricity (e) = 0.77
True anomaly (θ) = 37°
Flight path angle (γ ) = atan((esinθ)/(1 + ecosθ))
= atan((0.77*sin(37))/(1 + 0.77*cos(37)))
= 16.01°
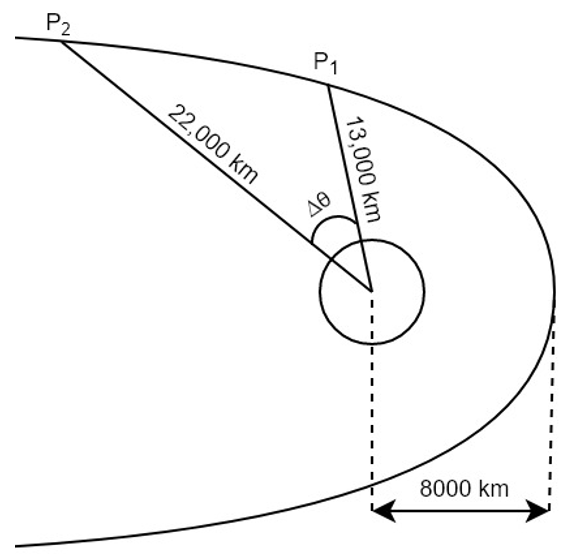
7. Chandrayaan-2 is travelling in a parabolic orbit around earth as shown in the figure below. What is the angle Δθ? Given, standard gravitational parameter of earth is 398,600 km3/s2.
a) 22.19°
b) 25.78°
c) 49.73°
d) 29.17°
View Answer
Explanation: Given,
Standard gravitational parameter (μ) = 398,600 km3/s2
Perigee distance (rp) = 8000 km
Distance from earth’s center to P1 (r1) = 13,000 km
Distance from earth’s center to P2 (r2) = 22,000 km
Specific angular momentum (h) = (2μrp)1/2
= (2*398,600*8000)1/2
= 79,859.88 km2/s
By rearranging the orbit equation, the true anomaly for P1 can be found as:
θ1 = acos(h2/(r1μ) – 1)
= acos(79,859.92/(13,000*398,600)-1)
= acos(0.231)
= 76.66°
Similarly, the true anomaly for P2 is:
θ2 = acos(h2/(r2μ) – 1)
= acos(79,859.92/(22,000*398,600)-1)
= acos(-0.273)
= 105.83°
Δθ = θ2 – θ1
= 105.83 – 76.66
= 29.17°
8. What is the specific energy of a spacecraft in an elliptical orbit around earth? Given, apogee and perigee distance from the surface of earth are 6250 km and 525 km respectively. The radius and standard gravitational parameter of earth are 6378 km and 398,600 km3/s2.
a) -30.3 km3/s2
b) 40.2 km3/s2
c) -10.9 km3/s2
d) 12.9 J/kg
View Answer
Explanation: Given,
Standard gravitational parameter (μ) = 398,600 km3/s2
Radius of earth (RE) = 6378 km
Semi-major axis (a) = (525 + 6250 + 6378)/2
= 6576.5 km
Specific energy (ε) = -μ/(2a)
= -398,600/(2*6576.5)
= -30.3 km3/s2
9. The energy equation describing orbital mechanics is also known as _______________ equation.
a) vis-viva
b) minores orbita
c) majores orbita
d) simplex visa
View Answer
Explanation: Vis-viva equation is the other name for energy equation for orbits. It is Latin for “living force”. The equation describes the conservation of energy of each orbit. Kinetic energy and Gravitational energy compensate for each other to conserve the overall energy.
10. For a circular orbit, the higher the radius of the orbit, the lower will be its specific energy?
a) True
b) False
View Answer
Explanation: False, because the specific energy will increase with increasing radius. The equation to describe specific energy is given by ε = -μ/(2r). Therefore, as r increases the specific energy becomes less negative.
More MCQs on Two-Body Orbital Mechanics:
- Two-Body Orbital Mechanics MCQ (Set 2)
- Two-Body Orbital Mechanics MCQ (Set 3)
- Two-Body Orbital Mechanics MCQ (Set 4)
- Two-Body Orbital Mechanics MCQ (Set 5)
Sanfoundry Global Education & Learning Series – Orbital Mechanics.
To practice all areas of Orbital Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
