This set of Orbital Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “In-Plane Orbit Changes”.
1. Which of these is not a part of in-plane orbit changes?
a) Hohmann transfer
b) Adjustment of perigee an apogee height
c) General coplanar transfer between circular orbits
d) Change of inclination of the orbits
View Answer
Explanation: When the satellite is launches, there’s often error in burnout altitude, speed, flight path angle and the exact orbit that was desired is not achieved. This is corrected by applying a small delta-v in the same plane to adjust the orbital parameters. The in-plane corrections include- Hohmann transfer, adjustment of perigee and apogee height, general coplanar transfer between circular orbits.
2. How will themajor axis be affected if the velocity at a point in the orbit is doubled leaving r unchanged?
a) Major-axis becomes twice
b) Major-axis becomes half
c) Major-axis is unaffected
d) Major-axis becomes one-fourth
View Answer
Explanation: The energy equation is given by:
ε = \(\frac{v^2}{2} – \frac{\mu}{r} = -\frac{\mu}{2a}\)
On rearranging the terms, we get:
v2 = μ(\(\frac{2}{r} – \frac{1}{a}\))
For finding how change in velocity affects the semi-major axis, we have to differentiate it:
da = \(\frac{2a^2}{\mu}\) vdv
Using the above relation, the major axis is given by 2a, thus the length of the orbit changes by twice this amount or 2da when the velocity at the orbit is doubled.
3. Which of these in-plane transfers is used to transfer the satellite between the circular coplanar orbits using an elliptical transfer orbit?
a) One-tangent transfer
b) Bi-elliptical transfer
c) Hohmann transfer
d) Phasing maneuver
View Answer
Explanation: The transfer between two circular coplanar orbits is carries out using Hohmann transfer. It is a way of moving the satellite to a high-altitude orbit from the parking orbit or the other way round. The transfer takes place using a transfer elliptical orbit in the same plane.
4. What is the energy of the transfer orbit required if the satellite moves from the first orbit at an altitude of 480 km to second orbit at 3000 km altitude?
a) -10.10 km2/s2
b) -15.55 km2/s2
c) -20.10 km2/s2
d) -24.55 km2/s2
View Answer
Explanation: Given, r1 = 480 + 6,378 = 6,858 km, r2 = 3,000 + 6,378 = 9,378 km
The semi-major axis of the transfer orbit is: 2at = r1 + r2
The energy of the orbit is given by the relation: E = –\(\frac{\mu}{2a}\)
Replacing the value of semi0major axis (a), we get: E = –\(\frac{\mu}{(r_1 + r_2)} = -\frac{398,600}{(6,858 + 9,378)}\) = -24.55 km2/s2.
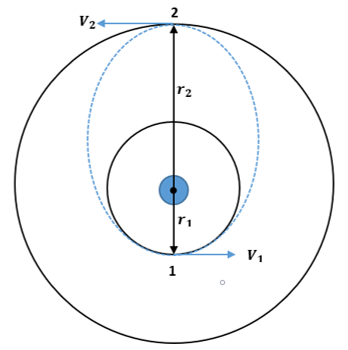
5. Which of these in-plane transfers is possible?
a) 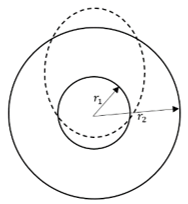
b) 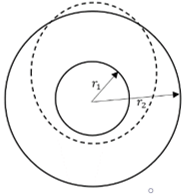
c) 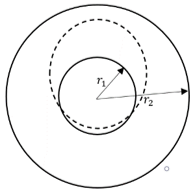
d) 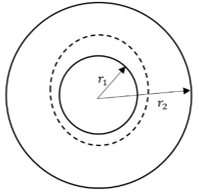
View Answer
Explanation: For a successful in-plane transfer, the transfer orbit must intersect both the smaller and the bigger orbits where r1 and r2 are the radius of inner and outer orbits, or it can at least be tangent to both the circular orbits.
6. Which of this parameter in an in-plane maneuver does not change?
a) Magnitude of velocity
b) Direction of velocity
c) Magnitude of angular momentum
d) Direction of angular momentum
View Answer
Explanation: An in-plane maneuver is the one which does not involve change in plane while changing satellite’s orbit. In- plane maneuver incorporates change in magnitude and direction of the velocity vector. Due to this change the magnitude of angular momentum vector also changes as \(\vec{h} = \vec{r} × \vec{v}\). But there is no change in the direction of the angular momentum vector as it is orthogonal to the orbital plane.
7. For a satellite to escape the pull of gravity, it has restrictions of flight path angle.
a) True
b) False
View Answer
Explanation: The escape condition has no restriction on the flight path angle. As long as the velocity is greater or equal to the escape velocity, it can escape the gravity’s pull at any angle. Only for circular orbits the flight angle has to be at an angle of 0 deg.
8. What is the energy of in-plane transfer orbit if the eccentricity of the orbit is 0.45 and the semi-major axis is 5,800 km?
a) -15.114 km2/s2
b) -34.362 km2/s2
c) -48.252 km2/s2
d) -52.141 km2/s2
View Answer
Explanation: Given, e = 0.45
Energy of the transfer orbit is given by:
Et = \(\frac{-\mu(1 – e^2)}{2p}\)
Where p is given by: p = a(1 – e2) = 5,800(1 – 0.452) = 4625.5 km
Et = \(\frac{-398,600 (1 – 0.45^2)}{2 × 4625.5}\) = -34.362 \(\frac{km^2}{s^2}\).
9. Periapsis radius of the transfer orbit must be equal to or greater than the radius of the inner orbit for an in-plan transfer.
a) True
b) False
View Answer
Explanation: The periapsis radius of the transfer orbit must be equal to or less than the radius of the inner orbit and the apoapsis radius must be equal to or exceed the radius of the outer orbit for the transfer orbit in an in-plane transfer.
10. What is the transfer orbit of an in-plane orbit whose semi latus rectum (p) is given as 6500 km?
a) 38,900 kgm2/s
b) 45,500 kgm2/s
c) 50,900 kgm2/s
d) 60,000 kgm2/s
View Answer
Explanation: Given, p = 6,500 km
The angular momentum for the elliptical transfer orbit is given as:
ht = \(\sqrt{\mu p} = \sqrt{398,600 × 6500}\) = 50,900\(\frac{kgm^2}{s}\).
Sanfoundry Global Education & Learning Series – Orbital Mechanics.
To practice all areas of Orbital Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
