This set of Orbital Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Two Body Problem”.
1. The two-body problem assumes both bodies as point masses.
a) True
b) False
View Answer
Explanation: True. Kinematic properties of the moving body relative to the stationary body can be calculated by assuming the bodies as point masses concentrated at their respective center of masses. Despite the bodies being rigid bodies, knowledge of point mass dynamics is all that is required. Rigid body dynamics is applied to calculate more complex data which is beyond the purpose of a two-body problem.
2. What is the area swept by a satellite in an elliptical orbit around earth at t = T/5, where T is the time period of the orbit? Given, semi-major axis and semi-minor axis of the orbit are 9,000 km and 4,000 km respectively.
a) 22.62 x 106 km2
b) 29.89 x 106 km2
c) 120.5 x 103 km2
d) 117.9 x 104 km2
View Answer
Explanation: Given,
Semi-major axis (a) = 9,000 km
Semi-minor axis (b) = 4,000 km
Area swept (at t = T/5) (A)=?
Due to similarity,
A/(T/3) = πab/T || Area of ellipse = πab
A = πab/5
= π*9,000*4,000/5
= 22.62 x 106 km2
3. What is the velocity of a satellite orbiting around moon in a circular orbit of altitude 100 km from moon’s surface. Given, standard gravitational parameter of moon is 4903 km3/s2 and radius of moon is 1738 km.
a) 2.089 km/s
b) 3.211 km/s
c) 1.633 km/s
d) 1.015 km/s
View Answer
Explanation: Given,
Standard gravitational parameter (μ) = 4903 km3/s2
Radius of moon (RM) = 1738 km
Altitude from surface of moon (z) = 100 km
Velocity of satellite (v) = (μ/(RM + z))1/2
= (4903/(1738+100))1/2
= 1.633 km/s
4. How long does it take for a satellite to travel between perigee and apogee? Apogee and perigee altitude from surface of the earth is 900 km and 400 km respectively. Earth’s radius and standard gravitational parameter is 6378 km and 398,600 km3/s2 respectively.
a) 7983.13 s
b) 2931.8 s
c) 4211.11 s
d) 5863.53 s
View Answer
Explanation: Given,
Perigee distance (rp) = 6378 + 400 = 6778 km
Apogee distance (ra) = 6378 + 900 = 7278 km
Semi-major axis (a) = (rp + ra)/2
= (6778 + 7278)/2
= 7028 km
Time period of the orbit (T) = 2πa3/2/μ1/2
= 2π*70283/2/398,6001/2
= 5863.53 s
Time taken to travel from perigee to apogee = T/2 = 5863.53/2 = 2931.8 s
5. What is the specific angular momentum of an elliptical orbit, if the flight path angle of the satellite in orbit at an instant is 15°? The satellite is travelling at a velocity of 10.7 km/s at the same instant and is parked at an altitude of 7048 km measured from earth’s center.
a) 70,234.12 km2/s
b) 72,876.32 km2/s
c) 61,456.23 km2/s
d) 4,536.32 km2/s
View Answer
Explanation: Given,
Velocity of satellite (v) = 10.7 km/s
Flight path angle (γ) =15°
Satellite distance (r) = 7048 km
Tangential velocity (vt) = vcos(γ) = 10.7*cos(15°) = 10.34 km/s
Specific angular momentum (h) = rvt = 7048*10.34 = 72,876.32 km2/s
6. What is the eccentricity of an orbit if tangential and radial velocity are 9.08 km/s and 2.01 km/s respectively. Specific angular momentum is 63,585 km2/s. Standard gravitational parameter is 398,600 km3/s2.
a) 0.423
b) 0.127
c) 0.934
d) 0.551
View Answer
Explanation: Given,
Radial velocity (vr)= 2.01 km/s
(vt) = 9.08 km/s
Specific angular momentum (h) = 63,585 km2/s
Satellite distance from earth’s center (r) = h/vt
= 63,585/9.08
= 7,002.75 km
From orbit equation,
ecos(θ) = h2/(μr) – 1
= 63,5852/(398,600*7002.75) – 1
= 0.448
esin(θ) = vr h/μ
= 2.01*63,585/398,600
= 0.321
esin(θ)/ecos(θ) = 0.321/0.448
θ = atan(0.716)
= 35.59°
Eccentricity (e) = 0.448/cos(θ)
= 0.551
7. Position, Velocity and Acceleration of a celestial body is as follows:
\(\vec{r}\) = 290\(\hat i\) + 640\(\hat j\) + 410\(\hat k\) (m)
\(\vec{v}\) = 90\(\hat i\) + 125\(\hat j\) 200\(\hat k\) (m/s)
\(\vec{a}\) = 14\(\hat i\) + 125\(\hat j\) 27\(\hat k\) (m⁄s2)
What is its radius of curvature?
a) 129.20 m
b) 158.12 m
c) 680.44 m
d) 456.89 m
View Answer
Explanation:
v = \(\sqrt{90^2 + 125^2 + 200^2}\) = 252.44 m/s
\(\hat u_t = \frac{\vec v}{v} = \frac{90\hat i + 125\hat j + 200\hat k}{252.44} \)= 0.357\(\hat i\) + 0.495\(\hat j\) + 0.79\(\hat k\)
at = \(\vec{a}\).\(\hat u_t\) = (14\(\hat i\) + 125\(\hat j\) 27\(\hat k\)) . (0.357\(\hat i\) + 0.495\(\hat j\) + 0.79\(\hat k\)) = 88.203 m/s2
a = \(\sqrt{14^2 + 125^2 + 27^2}\) = 128.65 m⁄s2
\(\vec{a}\) = at\(\hat u_t\) + an\(\hat u_n\)
an = \(\sqrt{a^2 – a_t^2} = \sqrt{128.65^2 – 88.203^2}\) = 93.65 m⁄s2
Radius of curvature can then be found as,
ρ = \(\frac{v^2}{a_n} = \frac{252.44^2}{93.65}\) = 680.44 m
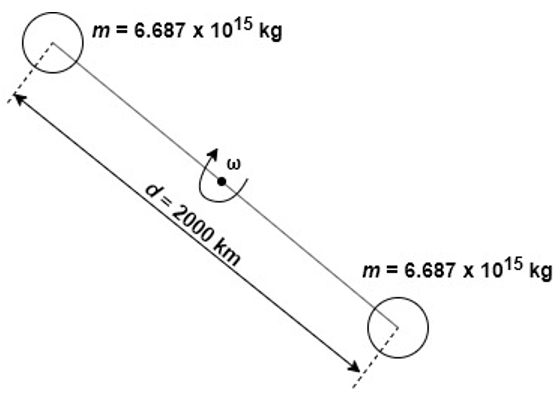
8. Two asteroids with a mass of 6.687 x 1015 kg each are only acted upon by each other’s gravitational pull. If they are separated by a constant distance of 2000 km. What is the angular velocity of the line joining them? Gravitational constant is 6.67 x 10-11 m3 kg-1 s-2.
a) 0.1221 rad/hr
b) 0.001202 rad/hr
c) 0.0027 rad/hr
d) 0.0195 rad/hr
View Answer
Explanation: Given,
Standard gravitational parameter (μ) = 398,600 km3/s2
Mass of asteroid (m) = 6.687 x 1015 kg
Distance between two asteroids (d) = 2000 km
Radius of rotation (r) = d/2 || Since both the masses are equal, the point of rotation must be halfway
Gravitational Force (Fg) = Gmm/d2
= (Gm2)/(4r2)
Centripetal Force (Fc) = mω2r
We know, Fg = Fc
(Gm2)/(4r2) = mω2r
Upon simplification,
Angular velocity (ω) = ((2Gm)/d3)1/2
= ((2*6.67*10-11*6.687*1015)/20003)1/2
= 3.339 x 10-7 rad/s
= 0.001202 rad/hr
9. For two-body problems, satellite motion is represented as __________ motion.
a) Curvilinear
b) Rectilinear
c) Rotary
d) Brownian
View Answer
Explanation: Curvilinear motion because all orbits/trajectories have a radius of curvature. Or in other words, all orbits are conic section and therefore curved. Rectilinear motion could be useful if a satellite moved in a straight line. Rotary motion also rotates, but it rotates along its own axis. Though most celestial bodies have rotary motion, it also does not apply to point masses (which is how bodies are assumed in two body problems). Brownian motion is a random motion of particles and has application in quantum world.
10. In the following equation, what are orbital constants? r = [h2/μ][1/(1 + ecosθ)].
a) h, μ and θ
b) Only μ
c) h and e
d) h, μ and e
View Answer
Explanation: h and e (specific angular momentum and eccentricity) are the orbital constants among all the letters in the orbit equation. μ (standard gravitational parameter) is a constant that is independent of the orbit and depends on the mass of the larger body. Whereas, true anomaly (θ) is not constant and is dependent on the spacecraft/satellite position relative to perigee line.
Sanfoundry Global Education & Learning Series – Orbital Mechanics.
To practice all areas of Orbital Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
