This set of Orbital Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Circular Orbits”.
1. There is no radial velocity component if a satellite is travelling in a circular orbit.
a) True
b) False
View Answer
Explanation: Tangential velocity is equal to the satellite velocity in a circular orbit since both the velocities travel along the same direction throughout the orbit. Therefore, there is no radial component. There is acceleration along the radial direction though which keeps the satellite in orbit without falling back to earth.
2. What is the velocity of a spacecraft in a circular orbit of 1,000 km from the surface of Mars? Radius of Mars is 3,389.5 km and its mass is 6.39 x 1023 kg.
a) 7.233 km/s
b) 4.525 km/s
c) 3.117 km/s
d) 3.989 km/s
View Answer
Explanation: Given,
Radius of spacecraft (r) = 1,000 + 3389.5
= 4389.5 km
Gravitational parameter (μ) = GM
= 6.674 x 10-20 x 6.39 x 1023
= 42,646.86 km3/s2
Spacecraft velocity (v) = (μ/r)1/2
= (42,646.86/4389.5)1/2
= 3.117 km/s
3. What is the sidereal time period of a probe in a circular orbit around Mars? The probe is orbiting at an altitude of 500 km from the surface of Mars. Radius of Mars is 3,389.5 km and its mass is 6.39 x 1023 kg.
a) 2.48 hrs
b) 2.05 hrs
c) 2.16 hrs
d) 1.89 hrs
View Answer
Explanation: Given,
Gravitational parameter (μ) = GM
= 6.674 x 10-20 x 6.39 x 1023
= 42,646.86 km3/s2
Probe radius (r) = 3389.5 + 500
= 3889.5 km
Time period (T) = 2πμ-1/2r3/2
= 2*π*(42,646.86)-1/2*(3889.5)3/2
= 7,380.35 s
= 2.05 hrs
4. What is the specific energy of a satellite in circular orbit of radius 7078 km around earth? Given, gravitational parameter of earth is 398,600 km3/s2.
a) -90.14 km2/s2
b) -180.15 km2/s2
c) -30.13 km2/s2
d) -28.16 km2/s2
View Answer
Explanation:
Specific energy = -μ/(2r)
= -398,600/(2*7078)
= -28.1577 km2/s2
5. What is the angular velocity of earth given one sidereal day of earth is 23 hours 55 minutes and 48 seconds?
a) 7.293 x 10-5 rad/s
b) 7.05 x 10-5 rad/s
c) 4.236 x 10-5 rad/s
d) 1.223 x 10-3 rad/s
View Answer
Explanation:
Sidereal time = 23*60*60 + 55*60 +48
= 86,148 s
Angular velocity = (2π)/Sidereal time
= (2π)/86,148
= 7.293 x 10-5 rad/s
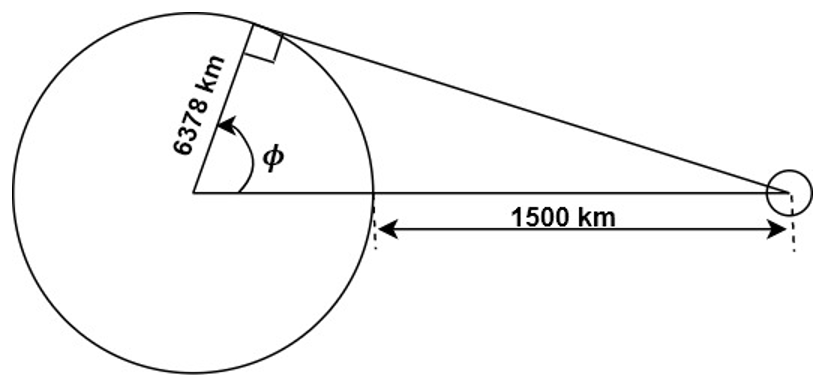
6. What is the maximum latitude visible from Geostationary orbit as shown in figure?
a) 76.98°
b) 45°
c) 35.94°
d) 39.12°
View Answer
Explanation: It is clear from the figure,
Maximum Latitude (Φ) = acos (6378/(6378+1500))
= 35.94°
7. A sidereal day for Mars is 24.623 hours. ISRO is planning to put a satellite in geostationary orbit around Mars. What should be the altitude from the surface of Mars to achieve this goal? Radius of Mars is 3,389.5 km and gravitational parameter is 42,828 km3/s2.
a) 17,038.14 km
b) 25,012.11 km
c) 20,427.64 km
d) 13648.64 km
View Answer
Explanation:
Angular velocity of Mars (ω) = (2π/(24.623*60*60)
= 7.088 x 10-5 rad/s
Velocity of spacecraft is given by,
v = (μr)1/2
v = ωr
Solving for r,
Spacecraft radius (r) = (μ/ω2)1/3
= (42,828/(7.088×10-5)2)1/3
= 20,427.65 km
Spacecraft altitude (z) = r – RM
= 20,427.65 – 3,389.5
= 17,038.14 km
8. What is the additional speed required to escape from earth’s GEO? GEO altitude from earth’s surface is 35,786 km. Earth’s radius is 6,378 km.
a) 1.274 km/s
b) 4.348 km/s
c) 3.075 km/s
d) 2.091 km/s
View Answer
Explanation:
Radius of satellite (r) = 6,378 + 35,786
= 42,164 km
Satellite velocity (v) = (μ/r)1/2
= (398,600/42,164)1/2
= 3.0747 km/s
Escape velocity = 21/2 v
= 21/2 * 3.0747
= 4.3482 km/s
Additional velocity (Δv) = 4.3482 – 3.0747
= 1.2735 km/s
9. What is the flight path angle of a satellite in circular orbit of 30,000 km from earth’s surface and a true anomaly of 45°?
a) 22.5°
b) 0°
c) 45°
d) 27°
View Answer
Explanation: Since, the tangential velocity equals to the satellite velocity at any point across a circular orbit, the flight path angle is always zero. Regardless, of what the true anomaly or height of the satellite, in a circular orbit the flight path angle is zero.
10. What is the eccentricity of a GEO?
a) 1.01
b) 0.87
c) 1.0
d) 0.0
View Answer
Explanation: A geostationary orbit (GEO) is an orbit over a planet in which a satellite has a fixed position over the planet. This makes the orbital shape of GEO exactly as the shape of the planet. Since, all planets are spherical in shape their cross-sections are circular. Hence, the GEO is a circular orbit with eccentricity of 0. It might be slightly elliptical but for the sake of simplicity it can be assumed to circular.
Sanfoundry Global Education & Learning Series – Orbital Mechanics.
To practice all areas of Orbital Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
