This set of Signals & Systems Multiple Choice Questions & Answers (MCQs) focuses on “Average Power and Energy of a Signal”.
1. For the signal \(x (t) = δ(t) – \frac{4}{3} e^{-t} \,u(t) + \frac{1}{3} e^{2t} \,u(t)\). It has how many poles and zeroes at infinity?
a) 1, 0
b) 2, 2
c) 2, 0
d) 0, 0
View Answer
Explanation: Since the degree of the numerator and denominator of X(s) are equal as shown below,
\(X(s) = 1 – \frac{4}{3} \frac{1}{s+1} + \frac{1}{3} \frac{1}{s-2}\)
\(= \frac{(s-1)^2}{(s+1)(s-2)}\)
∴ X(s) has neither poles nor zeroes at infinity.
2. The resultant signal obtained after frequency convolution along with constant multiplier \(\frac{1}{2πj}\) of the signals whose Laplace transforms are given by, \(\frac{1}{s+2}\) and \(\frac{1}{s+1}\).
a) e-2t + e-t
b) e-2t
c) e-3t
d) e-t
View Answer
Explanation: f3 (t) = f1 (t). f2 (t)
The Laplace transform of f3 (t) is \(\frac{1}{2πj}\) F1(s) * F2(s)
Then, F1(s) = \(\frac{1}{s+2}\)
∴ f1 (t) = e-2t u(t)
F2(s) = \(\frac{1}{s+1}\)
∴ f2 (t) = e-t u(t)
∴ f3 (t) = e-3t (for all t>0).
3. Given signal given, \( y (t) = 2sin (\frac{2}{3} t) + 4sin (\frac{1}{4} t – \frac{π}{4}) + 6sin (\frac{1}{3} t – \frac{π}{5}) + 8sin (\frac{1}{2} t – \frac{π}{7}\)). The period of y(t) is ________________
a) 12 π
b) 24 π
c) 8 π
d) 16 π
View Answer
Explanation: ω1 = \(\frac{2}{3}\)
Or, T1 = \(\frac{2π}{ω_1}\) = 3π
Again, ω2 = \(\frac{1}{4}\)
Or, T2 = \(\frac{2π}{ω_2}\) = 8π
Again, ω3 = \(\frac{1}{3}\)
Or, T3 = \(\frac{2π}{ω_3}\) = 6π
And, ω4 = \(\frac{1}{2}\)
Or, T4 = \(\frac{2π}{ω_4}\) = 4π
∴ T = LCM (3π, 8 π, 6π, 4π)
∴ T = 24π.
4. The signal power of the periodic rectangular pulses of height 1 and width 1, is _______________
a) 0.25 W
b) 0.75 W
c) 0.5 W
d) 1 W
View Answer
Explanation: The signal power in the given signal using Parsevals’s relation is
\(P = \frac{1}{t} \int_0^T x^2 (t) \,dt\)
\(= \frac{1}{2} \int_0^1 1.dt\)
= 0.5 W.
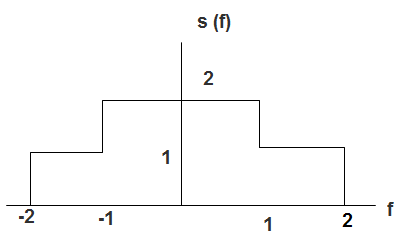
5. Power spectral density of the signal given below is _______________
a) 0
b) 6
c) ∞
d) -6
View Answer
Explanation: P = \(\int_{-∞}^∞ s(f)d(f)\)
= \(\int_{-2}^{-1} 1 \,df + \int_{-1}^1 2 \,df + \int_1^2 1 \,df\)
= 1(-1 + 2) + 2(1 + 1) + 1(2 – 1)
= 1 + 4 + 1 = 6.
6. A periodic signal has power \(\frac{P}{4}\) equal to average energy per period then rms value of signal is given by ________________
a) \(\frac{\sqrt{P}}{4}\)
b) \(\frac{P}{4}\)
c) \(\frac{P}{2}\)
d) \(\frac{\sqrt{P}}{2}\)
View Answer
Explanation: For an energy signal if the average energy per period is P, then the rms value which corresponds to a DC signal is equal to \(\sqrt{P}\).
∴ \(\frac{P}{4}\) –> x(t), then xrms (t) –> \(\frac{\sqrt{P}}{2}\).
7. For a LTI system consisting of two integrators, the output of the first integrator is inverted and fed as input to the sigma at beginning and output of the second integrator is also inverted and fed as input to the sigma at the beginning. The input is x (t) and output y (t), the transfer function is ______________
a) \(\frac{1}{s+4}\)
b) \(\frac{1}{s^2+4s+3}\)
c) \(\frac{1}{s^2-4s-3}\)
d) \(\frac{1}{s^2-4s+3}\)
View Answer
Explanation: Transfer function of linear loop = \(\displaystyle\frac{\frac{1}{s}}{1 + \frac{4}{s}}\)
= \(\frac{1}{s+4}\)
∴ Transfer function of the overall system = \(\displaystyle\frac{\frac{1}{s(s+4)}}{1 + \frac{3}{s(s+4)}}\)
= \(\frac{1}{s^2+4s+3}\).
8. A system has a block G1(s) which has input x (s) and output y1(s). This output is fed as input to a second block G2(s) which has output y2(s). For this system, G1(s) = \(\frac{s^{-1}}{1 + 2s^{-1} + s^{-2}}\).
G2(s) for the given system to be invertible is given by _______________
a) \(\frac{s}{1+2s+s^2}\)
b) \(\frac{1+2s+s^2}{s}\)
c) \(\frac{1}{1+2s+s^2}\)
d) 1+2s+s2
View Answer
Explanation: Given that G2(s) should be the inverse of G1(s).
∴ G2(s) = \(G_1^{-1} (s)\)
Or, G1(s) = \(\frac{s^{-1}}{1 + 2s^{-1} + s^{-2}}\)
∴ G2(s) = \(G_1^{-1} (s) = \frac{1+2s+s^2}{s}\).
9. The convolution y [n] = x [n] * h [n], where x [n] = {1,2,4} and h [n] = {1,1,1,1,1} is ________________
a) {1,3,7,7,7,6,4}
b) {1,3,3,7,7,6,4}
c) {1,2,4}
d) {1,3,7}
View Answer
Explanation: Given x [n] = {1, 2, 4} and h [n] = {1, 1, 1, 1, 1}.
Now, y [n] is the convolution of x [n] and h [n].
Hence, y [n] = {1, 3, 7, 7, 7, 6, 4}.
10. Given a periodic function having half wave symmetry. Then the function is ________________
a) An even function
b) An odd function
c) Both odd and even functions
d) Neither odd nor even functions
View Answer
Explanation: Let the time period be T then, f (t) = f (t ± T)
The function has half wave symmetry i.e., f (t) = -f \((t + \frac{T}{2})\).
11. The signal power of the signal x (t) = 2sin 2t + 4sin 4t + 6cos 4t + 2cos 2t with period 0.5 is ________________
a) 30 W
b) 36 W
c) 60 W
d) 12 W
View Answer
Explanation: Signal power = 0.5(22 + 42 + 62 + 22)
= 0.5(4 + 16 + 36 + 4)
= 0.5(20 + 40) = 30 W.
12. A signal is a power signal if the signal has average power equal to __________
a) Infinite
b) Finite
c) Zero
d) Does not depend on the average power value
View Answer
Explanation: A signal is said to be a power signal if and only if the average power of the signal is finite. In other words, we can say that a signal is a power signal if the energy of the signal is infinite, i.e., E = ∞.
13. A signal is an energy signal if the signal has average energy equal to __________
a) Infinite
b) Finite
c) Zero
d) Does not depend on the average energy value
View Answer
Explanation: A signal is said to be an energy signal if and only if the average energy of the signal is finite. In other words, we can say that a signal is an energy signal if the average power of the signal is infinite, i.e., P = ∞.
14. The energy in the time-domain representation of a signal is the same as in the frequency domain representation normalized by ___________
a) 2π
b) π
c) \(\frac{π}{2}\)
d) \(\frac{π}{4}\)
View Answer
Explanation: The solution lies in the basic definition of Parseval’s theorem.
We know that Parseval’s energy and power theorem states that, the energy in the time-domain representation of a signal is equal to the energy in the frequency domain representation normalized by 2π.
15. The system characterized by the equation y (t) = ax (t) + b is ____________
a) Linear for any value of b
b) Linear if b>0
c) Linear if b<0
d) Non-linear
View Answer
Explanation: The system is non-linear. The principle of homogeneity states that if for any input signal X (t), i.e. scaling any input signal scales the output signal by the same factor, then the signal X (t) is homogeneous. Because x (t) does not lead to y (t) = 0, which is a direct violation of the principle of homogeneity.
Sanfoundry Global Education & Learning Series – Signals & Systems.
To practice all areas of Signals & Systems, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
