This set of Signals & Systems Multiple Choice Questions & Answers (MCQs) focuses on “Region of Convergence”.
1. The impulse response h (t) of a LTI system is given by h (t) = exp (-2t) u (t) where, u (t) denotes the unit step function. The frequency response H(ω) is ____________
a) \(\frac{1}{1+j2ω}\)
b) \(\frac{sinω}{ω}\)
c) \(\frac{1}{2+jω}\)
d) \(\frac{jω}{2+jω}\)
View Answer
Explanation: Impulse response h (t) = e-2t u (t)
Taking Fourier transform, H (ω) = \(\int_{-∞}^∞ e^{-2t} \,u(t) e^{-jωt} \,dt\)
= \(\int_0^∞ e^{-2t} e^{-jωt} \,dt\)
= \(\int_0^∞ e^{-(2+jω)t} \,dt\)
= \(\frac{1}{2+jω}\).
2. The impulse response h (t) of a LTI system is given by h (t) = exp (-2t) u (t) where, u (t) denotes the unit step function. The output of this system to the sinusoidal input x(t) = 2 cos(2t) for all t, is _____________
a) 0
b) 2-0.25 cos(2t-0.125π)
c) 2-0.5 cos(2t-0.125π)
d) 2-0.5 cos(2t-0.25π)
View Answer
Explanation: X (t) = 2 cos2t
And ω=2 rad/s
H (ω) = \(\frac{1}{2+jω}\)
|H (ω)| = \(\frac{1}{\sqrt{z^2+ω^2}} = \frac{1}{2\sqrt{2}}\)
Hence y (t) = |H (ω)| × 2 cos [2t + *H (ω)] = \(\frac{1}{2\sqrt{2}} × 2 cos(2t – \frac{π}{4})\)
= 2-0.5 cos (2t-0.25π).
3. The ROC of u(n) = \(_k^nC\) is __________
a) | z | > 1
b) | z | < 1
c) -1 < | z | < 1
d) -1 < | z |
View Answer
Explanation: Z [u (n)] = \(∑_{-∞}^∞\) \(_k^nC z^{-n}\)
= \(∑_{n=k}^∞\) \( _{k}^{n}C 2^n z^{-n}\)
\(∴ Z[u(n)] = ∑_{r=0}^∞\) \( ^{k+r}_{k}C z^{-(k+r)}\)
= \(z^{-k} ∑_{r=0}^∞\)\( _r^{k+r}C z^{-(r)}\)
= \(z^{-k} (1-1/z)^{-(k+1)}\)
The series is convergent for | 1/z | < 1 i.e., for | z | > 1
Hence, ROC is | z | > 1.
4. The Radius of convergence of f(n) = 5n/n!, n≥0 is __________
a) -2<|z|<2
b) Z-plane
c) | z |<2
d) |z| = 2
View Answer
Explanation: \(∑_{n=0}^∞ \frac{5^n}{n!}.z^{-n}\)
= \(∑_0^∞ \frac{(5/z)^n}{n!}\)
= \(1 + (\frac{5}{z}) + \frac{1}{2!} (\frac{5}{z})^2 + \frac{1}{3!} (\frac{5}{z})^3 + ……\)
The above series is convergent for all values of z.
Hence, the radius of convergence is the entire z-plane.
5. The ROC of u(n) = 4n, for n<0; 2n, for n≥0 is ___________
a) 0<z<1
b) z<4
c) 2<z
d) 2<z<4
View Answer
Explanation: \(Z [u (n)] = ∑_{-∞}^∞ u(n) Z^{-n}\)
= \(∑_{-∞}^{-1} 4^n Z^{-n} + ∑_{n=0}^∞ 2^n Z^{-n}\)
= \(\frac{z}{4} \Big\{1 + \frac{z^1}{4} + \frac{z^2}{4} +⋯….\Big\} + \Big\{1 + \frac{2}{z} + \frac{2^2}{z} + ….\Big\}\)
= \(\frac{z}{4}. \frac{1}{1-\frac{z}{4}} + \frac{1}{1 – \frac{2}{z}}\)
= \(\frac{z}{4-z} + \frac{z}{z-2}\)
= \(\frac{2z}{(4-z)(z-2)}\)
Now, the above series will be convergent if | \(\frac{z}{4}\) |<1 and | \(\frac{2}{z}\) |<1.
That is 2<z<4.
6. The system under consideration is an RC low-pass filter with R = 1 kΩ and C = 1 µF. Let H (f) denotes the frequency response of the RC, low-pass filter. Let t1(f) be the group delay function of the given RC low-pass filter and f2 = 100 Hz. Then tg(f2) in ms is ___________
a) 0.717
b) 7.17
c) 71.7
d) 4.505
View Answer
Explanation: H (ω) = \(\frac{1}{1+jωRC}\)
Now, θ (ω) = – tan-1(ωRC)
Group delay = tg (ω) = – \(\frac{d θ(ω)}{dω}\)
= – \(\frac{d tan^{-1} (ωRC)}{dω}\)
∴ tg (ω) = \(\frac{RC}{1+ω^2 R^2 C^2}\)
Now, tg (f) = \(\frac{RC}{1+4π^2 f^2 R^2 C^2}\)
So, tg (f2) = \(\frac{RC}{1+4π^2 f_2^2 R^2 C^2}\) = 0.717 ms.
7. Given that X(s) is the Laplace transform of the signal cos 2t u (t). The time signal corresponding to (s+1) X(s) is _________________
a) (cos 2t – 2 sin 2t) u (t)
b) (cos 2t + \(\frac{sin2t}{2}\)) u (t)
c) (cos 2t + 2 sin 2t) u (t)
d) (cos 2t – \(\frac{sin2t}{2}\)) u (t)
View Answer
Explanation: We know that, s X (s) + X(s) is having Laplace transform \(\frac{dx(t)}{dt}\) + x (t)
Or, y (t) = (cos 2t – 2 sin 2t) u (t) .
8. Given that X(s) is the Laplace transform of the signal cos 2t u (t). The signal X(3s) corresponds is _______________
a) cos(\(\frac{2}{3}\) t) u (t)
b) \(\frac{1}{3}\) cos(\(\frac{2}{3}\) t) u (t)
c) cos6t u(t)
d) \(\frac{1}{3}\) cos6t u(t)
View Answer
Explanation: We know that the time signal of X (\(\frac{s}{a}\)) = a x (at)
Here, a = \(\frac{1}{3}\)
∴ X (3s) = \(\frac{1}{3}\) cos(\(\frac{2}{3}\) t) u (t).
9. The value of the radius of convergence of f(n) = 2n, n<0 is ____________
a) 0<| z |<1
b) -2<| z |
c) | z |<2
d) z-plane
View Answer
Explanation: Z [f (n)] = \(∑_{-∞}^∞ f(n) z^{-n}\)
= \(\frac{z}{2} + \frac{z^2}{2} + \frac{z^3}{2} + …. ∞\)
= \(\frac{z}{2}(1 + \frac{z}{2} + \frac{z^2}{2} + …..∞)\)
= \(\frac{1}{1-\frac{z}{2}} . \frac{z}{2} = \frac{z}{2-z}\)
The series is convergent if | \(\frac{z}{2}\) |<1, that is | z |<2
Hence, ROC is | z |<2.
10. The impulse response of a LTI system which is continuous is H (t) = e-|t|. The system is ___________
a) Causal and stable
b) Causal but not stable
c) Stable but not causal
d) Neither causal nor stable
View Answer
Explanation: For t<0,
H (t) ≠ 0
Therefore the system is not causal
Again, \(∫_{-∞}^∞ | h(t)| \,dt = \frac{1}{3}\) < ∞
∴ The system is stable.
11. For the system, y (t) = u{x (t)} which of the following holds true?
a) System is Linear, time-invariant, causal and stable
b) System is time-invariant, causal and stable
c) System is causal and stable
d) System is stable
View Answer
Explanation: Let x1(t) = v (t), then y1 (t) = u {v (t)}
Let x2(t) = k v (t), then y2 (t) = u {k v (t)} = k y1 (t)
Hence, non-linear
y1 (t) = u {v (t)}
y2 (t) = u {v (t-t0)} = y1 (t-t0)
Hence, time-invariant
Since the response at any time depends only on the excitation at time t=t0, and not on any further values, hence causal.
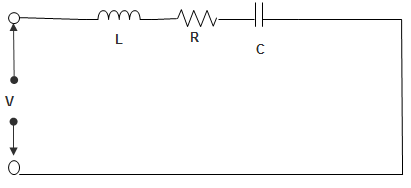
12. Given, R = 10 Ω, L = 100 mH and C = 10 μF. Selectivity is ____________
a) 10
b) 1.2
c) 0.15
d) 0.1
View Answer
Explanation: Selectivity = \(\frac{1}{Q}\)
Q = \(\frac{ωL}{R} = \frac{1000×100×10^{-3}}{10}\)
∴ Q = 10
So, Selectivity = 0.1.
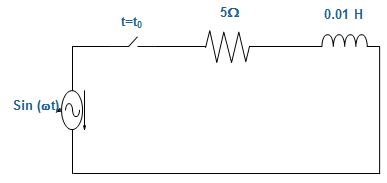
13. For the circuit given below, if the frequency of the source is 50 Hz, then a value of to which results in a transient free response is _________________
a) 0
b) 1.78 ms
c) 7.23 ms
d) 9.21 ms
View Answer
Explanation: T = \(\frac{L}{R}\)
Or, T = \(\frac{0.01}{5}\) = 0.002 s = 2 ms
For the ideal case, transient response will die out with time constant.
Practically, T will be less than 2 ms.
14. A series RC circuit excited by voltage V is __________
a) A memory less system
b) A causal system
c) A dynamic system
d) Static system
View Answer
Explanation: Dynamic systems are those systems which consist of memory. In the series RC circuit excited by voltage V, the capacitor C is an energy storing element which acts as a memory for the circuit. Therefore since system has memory it is not a memoryless system. Also, a causal system depends only on the past and present value. But since the future value of the charge is also under consideration in this type of circuit, so the system is not causal. Since charge moves about in the circuit due to the applied voltage V, hence the system is not static system. Therefore the system is a dynamic system.
15. The steady state value of F (t), if it is known that F(s) = \(\frac{b}{s(s+1)(s+a)}\), where a>0, is ________________
a) \(\frac{b}{a}\)
b) \(\frac{a}{b}\)
c) 1
d) Cannot be determined
View Answer
Explanation: F (∞) = lims→0 s F(s)
= lims→0 \(\frac{sb}{s(s+1)(s+a)}\)
= lims→0 \(\frac{b}{(s+1)(s+a)}\)
= \(\frac{b}{a}\).
Sanfoundry Global Education & Learning Series – Signals & Systems.
To practice all areas of Signals & Systems, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
