This set of Advanced Signals & Systems Questions and Answers focuses on “Miscellaneous Examples on Fourier Series”.
1. A signal g (t) = 10 sin (12πt) is ___________
a) A periodic signal with period 6 s
b) A periodic signal with period \(\frac{10}{6}\) s
c) A periodic signal with period \(\frac{1}{6}\) s
d) An aperiodic signal
View Answer
Explanation: 10 sin (12πt) = A sin ωt
∴ω = 12π
∴ 2πf = 1
So, fundamental frequency = 6
Hence, fundamental period = \(\frac{1}{6}\) s.
2. A voltage having the waveform of a sine curve is applied across a capacitor. When the frequency of the voltage is increased, what happens to the current through the capacitor?
a) Increases
b) Decreases
c) Remains same
d) Is zero
View Answer
Explanation: The current through the capacitor is given by,
IC = ωCV cos (ωt + 90°).
As the frequency is increased, IC also increases.
3. What is the steady state value of F (t), if it is known that \(F(s) = \frac{2}{s(S+1)(s+2)(s+3)}\)?
a) \(\frac{1}{2}\)
b) \(\frac{1}{3}\)
c) \(\frac{1}{4}\)
d) Cannot be determined
View Answer
Explanation: From the equation of F(s), we can infer that, a simple pole is at origin and all other poles are having negative real part.
∴ F(∞) = lim s→0 sF(s)
= lim s→0 \(\frac{2s}{s(S+1)(s+2)(s+3)}\)
= \(\frac{2}{s(S+1)(s+2)(s+3)}\)
= \(\frac{2}{6} = \frac{1}{3}\).
4. What is the steady state value of F (t), if it is known that F(s) = \(\frac{10}{(s+1)(s^2+1)}\)?
a) -5
b) 5
c) 10
d) Cannot be determined
View Answer
Explanation: The steady state value of this Laplace transform is cannot be determined since; F(s) is having two poles on the imaginary axis (j and –j). Hence the answer is that it cannot be determined.
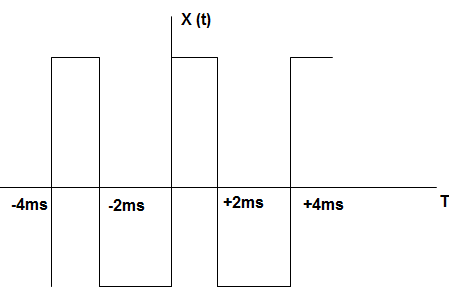
5. A periodic rectangular signal X (t) has the waveform as shown below. The frequency of the fifth harmonic of its spectrum is ______________
a) 40 Hz
b) 200 Hz
c) 250 Hz
d) 1250 Hz
View Answer
Explanation: Periodic time = 4 ms = 4 × 10-3
Fundamental frequency = \(\frac{10^3}{4}\) = 250 Hz
∴ Frequency of the fifth harmonic = 250 × 5 = 1250 Hz.
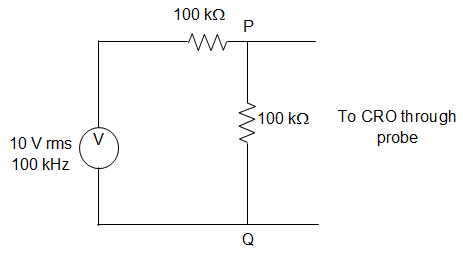
6. A CRO probe has an impedance of 500 kΩ in parallel with a capacitance of 10 pF. The probe is used to measure the voltage between P and Q as shown in the figure. The measured voltage will be?
a) 3.53 V
b) 3.47 V
c) 5.54 V
d) 7.00 V
View Answer
Explanation: \(X_C = \frac{1}{jCω} = \frac{-j}{2 × 3.14 × 100 × 10^3 × 10 × 10^{-12}}\)
Applying KCL at the node,
\(\frac{V_a-10}{100} + \frac{V_a}{100} + \frac{V_a}{500} + \frac{V_a}{-j159}\)
∴ Va = 4.37∠-15.95°.
7. The Fourier series coefficient of the signal z(t) = Re{x(t)} is ____________
a) \(\frac{X[k]+X[-k]}{2}\)
b) \(\frac{X[k]-X[-k]}{2}\)
c) \(\frac{X[k]+X^* [-k]}{2}\)
d) \(\frac{X[k]-X^* [-k]}{2}\)
View Answer
Explanation: Re{x (t)} = \(\frac{x(t)+x^* (-t)}{2}\)
The Fourier coefficient of x* (t) is
X1[k] = \(\frac{1}{T}\) ∫ x* (t)e-jkωt dt = \(X_1^*\) [-k]
Or, \(X_1^*\) [k] = \(\frac{1}{T}\) ∫ x(t)ejkωt dt = X [-k]
So, X1[k] = \(X_1^*\) [-k]
∴ Z[k] = \(\frac{X[k]+X^* [-k]}{2}\).
8. The Fourier series expansion of a real periodic signal with fundamental frequency f0 is given by gp (t) = \(∑_{n=-∞}^∞ C_n e^{j 2πnf_0 t}\). Given that C3 = 3 + j5. The value of C-3 is ______________
a) 5 + 3j
b) -5 + 3j
c) -3 – j5
d) 3 – j5
View Answer
Explanation: Given that C3 = 3 + j5.
We know that for real periodic signal C-k = \(C_k^*\)
So, C-3 = \(C_3^*\) = 3 – j5.
9. A signal e-at sin (ωt) is the input to a real linear time invariant system. Given K and ∅ are constants, the output of the system will be of the form Ke-bt sin (vt + ∅). The correct statement among the following is __________
a) b need not be equal to a but v must be equal to ω
b) v need not be equal to ω but b must be equal to a
c) b must be equal to a and v must be equal to ω
d) b need not be equal to a and v need not be equal to ω
View Answer
Explanation: For a system with input e-at sin (ωt) and output Ke-bt sin (v t + ∅), frequency (v) to output must be equal to input frequency (ω) while b will depend on system parameters and need not be equal to a.
10. Let us suppose that the impulse response of a causal LTI system is given as h (t). Now, consider the following two statements:
Statement 1- Principle of superposition holds
Statement 2- h (t) = 0(for t<0)
Which of the following is correct?
a) Statement 1 is correct and Statement 2 is wrong
b) Statement 2 is correct and Statement 1 is wrong
c) Both Statement 1 and Statement 2 are wrong
d) Both statement 1 and Statement 2 are correct
View Answer
Explanation: As we know that linear system possesses superposition theorem.
Hence, Statement 1 satisfies the given equation. We also know that time invariant condition depend on time.
Hence, Statement 2 satisfies the given equation.
11. The Fourier series representation of an impulse train denoted by s(t) = \(∑_{n=-∞}^∞ δ(t-nT_0)\) is given by _____________
a) \(\frac{1}{T_0} ∑_{n=-∞}^∞ exp(-\frac{j2πnt}{T_0}) \)
b) \(\frac{1}{T_0} ∑_{n=-∞}^∞ exp(-\frac{jπnt}{T_0})\)
c) \(\frac{1}{T_0} ∑_{n=-∞}^∞ exp(\frac{jπnt}{T_0}) \)
d) \(\frac{1}{T_0} ∑_{n=-∞}^∞ exp(\frac{j2πnt}{T_0}) \)
View Answer
Explanation: s (t) = \(∑_{n=-∞}^∞ C_n e^{jnω_0 t}\), where ω0=(2T/T0)
And Cn = \(\frac{1}{T_0} \displaystyle\int_{-\frac{T_0}{2}}^{\frac{T_0}{2}} δ(t) e^{-jnω_0 t} \,dt\)
= \(\frac{1.e^{-jnω_0 t}}{T_0}\)
So, Fourier series representation = \(\frac{1}{T_0} ∑_{n=-∞}^∞ exp(-\frac{jπnt}{T_0})\).
12. For which of the following a Fourier series cannot be defined?
a) 3 sin (25t)
b) 4 cos (20t + 3) + 2 sin (710t)
c) exp(-|t|) sin (25t)
d) 1
View Answer
Explanation: 3 sin (25) = 25
4 cos (20 + 3) + 2sin (710) sum of two periodic function is also periodic function
For 1 which is a constant, Fourier series exists.
For exp (-|t|) sin (25t), due to decaying exponential decaying function, it is not periodic. So Fourier series cannot be defined for it.
13. The RMS value of a rectangular wave of period T, having a value of +V for a duration T1 (< T) and −V for the duration T − T1 = T2, equals _____________
a) V
b) \(\frac{V}{\sqrt{2}}\)
c) \(\frac{T_1-T_2}{T}\) V
d) \(\frac{T_1}{T_2}\) V
View Answer
Explanation: Period = T = T1 + T2
RMS value = \(\sqrt{\frac{1}{T} ∫_0^T x^2 (t)dt}\)
= \(\sqrt{\frac{1}{T}[V^2.(T_1 – 0) + V^2 (T – T_1)]}\)
= \(\sqrt{V^2}\)
= V.
14. A periodic square wave is formed by rectangular pulses ranging from -1 to +1 and period = 2 units. The ratio of the power in the 7th harmonic to the power in the 5th harmonic for this waveform is equal to ____________
a) 1
b) 0.5
c) 2
d) 2.5
View Answer
Explanation: For a periodic square wave nth harmonic component ∝ \(\frac{1}{n}\)
Thus the power in the nth harmonic component is ∝ \(\frac{1}{n^2}\)
∴ Ratio of power in 7th harmonic to 5th harmonic for the given wage form = \(\frac{\frac{1}{7^2}}{\frac{1}{5^2}}\)
= \(\frac{25}{4}\) ≅ 0.5.
15. A useful property of the unit impulse 6 (t) is ________________
a) 6 (at) = a 6 (t)
b) 6 (at) = 6 (t)
c) 6 (at) = \(\frac{1}{a}\) 6(t)
d) 6(at) = [6(t)]a
View Answer
Explanation: Time-scaling property of 6(t)
We know that by this property,
6(at) = \(\frac{1}{a}\) 6(t), a>0
Sanfoundry Global Education & Learning Series – Signals & Systems.
To practice advanced questions and answers on all areas of Signals & Systems, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
