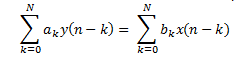This set of Signals & Systems Quiz focuses on “Discrete-Time Systems in the Time-Domain – 2”.
1. The difference equation for an Nth order discrete-time system is ___________
a) \(∑_{k=-∞}^∞\) ak y(n-k) = \(∑_{k=-∞}^∞\) bk x(n-k)
b) \(∑_{k=0}^∞\) ak y(n-k) = \(∑_{k=0}^∞\) bk x(n-k)
c) \(∑_{k=0}^N\) ak y(n-k) = \(∑_{k=0}^N\) bk x(n-k)
d) \(∑_{k=-∞}^0\) ak y(n-k) = \(∑_{k=-∞}^0\) bk x(n-k)
View Answer
Explanation: The difference equation for an Nth order discrete-time system is:
2. The response of any discrete time system can be decomposed as _____________
a) Total Response=Impulse+step
b) Total Response=Impulse+Ramp
c) Total Response=zero-output response
d) Total Response=zero-state response+zero-input response
View Answer
Explanation: There are two approaches to analyzing response of a system:
Direct solution of difference solution
Decomposing in terms of impulse signals
In the first method, the response of the system can be decomposed as:
Total Response = zero-state response + zero-input response.
3. Zero-state response of the system is _____________
a) Response of the system when initial state of the system is zero
b) Response of the system due to input alone
c) Response of the system due to input alone when initial state of the system is zero
d) Response of the system due to input alone when initial state is neglected
View Answer
Explanation: Zero-state response of the system is the response of the system due to input alone when the initial state of the system is zero. That is the system is relaxed at time n = 0.
4. Zero-input response is also known as ____________
a) zero-state response
b) Natural response
c) state-input response
d) Forced response
View Answer
Explanation: Natural response of the system is when the input x(n) = 0.
5. The general solution of natural response is of the form of _________
a) yh (n)= c1 λ1n+c2λ2n+⋯+cNλNn
b) yh (n)= c1 λ1n+c2λ2n+⋯+cNλNn
c) yh (n)= c1 λ12+c2λ22+⋯+cNλN2
d) yh(n)= c1 λ1n-c2λ2n+⋯+cNλNn
View Answer
Explanation: The general solution of natural response is of the form:
yh (n)= c1 λ1n+c2λ2n+⋯+cNλNn
The form will vary if the roots are repeating or complex.
6. Determine the natural response of the system: Difference equation is
y(n)-y(n-1)-2y(n-2)=x(n) and y(-1) = 1; y(-2) = 0
a) yh (n) = \(\frac{4}{3}\) (1)n – \(\frac{1}{3}\) (-1)n
b) yh (n) = \(\frac{4}{3}\) (-1)n – \(\frac{1}{3}\) (-1)n
c) yh (n) = \(\frac{4}{3}\) (2)n – \(\frac{1}{3}\) (-1)n
d) yh (n) = \(\frac{4}{3}\) (2)n – \(\frac{1}{3}\) (2)n
View Answer
Explanation: Natural Response of the system:
Homogenous equation ⇒ y(n)-y(n-1)-2y(n-2)=0
The homogenous solution: yh(n)= λn
⇒ λn– λ(n-1)-2λ(n-2)=0
⇒ λ(n-2) [λ2– λ1-2]=0
⇒ λ2– λ-2=0
⇒ λ2-2λ+λ-2=0
⇒ λ(λ-2)+1(λ-2)=0
⇒ (λ-2)(λ+1)=0
⇒ λ1=2,λ2=-1
General form of homogenous solution is
yh (n)= c1 (2)n+c2(-1)n (1)
⇒ y(0)= c1+c2 (2)
⇒ y(1)=2c1– c2 (3)
⇒ y(0)-y(-1)-2y(-2)=0
Given, y(-1) = 1 and y(-2) = 0
⇒ y(0)-1=0⇒y(0)=1
Similarly, y(1)-y(0)-2y(-1)=0⇒y(1)=1+2=3
∴ y(0) = 1 and y(1) = 3
Comparing the above values with equations (2) and (3)
⇒ c1+c2=1 and 2c1– c2=3
Solving the two equations we get, c1 = 4/3 and c2 = -1/3
7. Forced Response is solution of difference equation when ____________
a) Input is zero
b) Input is given and initial conditions are zero
c) Natural Response
d) Input is given and initial conditions are non-zero
View Answer
Explanation: Forced response is solution of difference equation when input is given and initial conditions are zero. Also known as zero-state response.
8. Forced response consists of _________
a) Homogenous solution and general solution
b) General solution alone
c) Homogenous solution and particular solution
d) Particular solution alone
View Answer
Explanation: Forced response consists of homogenous solution and particular solution.
Sanfoundry Global Education & Learning Series – Signals & Systems.
To practice all areas of Signals & Systems for Quizzes, here is complete set of 1000+ Multiple Choice Questions and Answers.
