This set of Signals & Systems Multiple Choice Questions & Answers (MCQs) focuses on “Power and Energy Signals”.
1. For any given signal, average power in its 6 harmonic components as 10 mW each and fundamental component also has 10 mV power. Then, average power in the periodic signal is _______________
a) 70
b) 60
c) 10
d) 5
View Answer
Explanation: We know that according to Parseval’s relation, average power is equal to the sum of the average powers in all of its harmonic components.
∴ Pavg = 10 × 6 = 60.
2. The property of Fourier Transform which states that the compression in time domain is equivalent to the expansion in the frequency domain is ____________
a) Duality
b) Scaling
c) Time scaling
d) Frequency shifting
View Answer
Explanation: From the time scaling property, we can infer that, time scaling is the property which states that compression in the time domain is equivalent to the expansion in the frequency domain.
3. The impulse response h[n] of a linear time-invariant system is h[n] = u [n+3] + u [n-2] – 2u [n-7] where, u[n] is the step unit response. The above system is ________________
a) Stable but not causal
b) Stable and causal
c) Causal but unstable
d) Unstable and not causal
View Answer
Explanation: \(∑_{k=-∞}^∞ h(k) = ∑_{k=-3}^∞ u(k+3) + ∑_{k=2}^∞ u(k-2) – 2∑_{k=7}^∞ u(k-7)\)
= \(∑_{k=-3}^6 1 + ∑_{k=2}^6 1\)
= 10 + 5
= 15 < ∞
For bounded input, we are getting bounded output. So system is stable.
The response depends on future value of input signal i.e. u (n+3). So, the system is not causal.
4. The final value of X(s) = \(\frac{12(s+1)}{s(s^2+4)}\) is _________
a) 1
b) 2
c) 3
d) Undetermined
View Answer
Explanation: Final value theorem is not applicable for poles on imaginary axis.
Given axis has poles at s = +j2, -j2 and s = 0.
Therefore, x (∞) is undetermined.
5. The Laplace transform of a signal is given as Y(s) = \(\frac{1}{s(s-1)}\), then the final value is ___________
a) -1
b) 0
c) 1
d) Unbounded
View Answer
Explanation: Final value theorem is applicable only when all the poles of the system lie in the left half of the s-plane.
Here, s=1 lies on the right s-plane pole.
Hence the final value is unbounded.
6. Given that, F(s) = \(\frac{w}{s^2+w^2}\). Re[s]>0. The final value of f(t) is ___________
a) 0
b) 1
c) [-1,1]
d) ∞
View Answer
Explanation: L-1 [F(S)] = sin wt
So, f (t) = sin wt
As sin lies between [-1, 1], so, final value of f (t) lies in [-1, 1].
7. A voltage LT is given as \(\frac{4s^2+3s+2}{7s^2+6s+5}\). It is applied across a 2H inductor having zero initial current. The current in the inductor at t = ∞ is ___________
a) 0
b) 1/5 A
c) 2/7 A
d) 2/5 A
View Answer
Explanation: We know that, i (∞) = lims→0 sI(s)
Now, V(s) = Ls I(s)
∴ i(s) = lims→0 \(\frac{V(s)}{L}\) = lims→0 \(\frac{1}{2}\Big[\frac{4s^2+3s+2}{7s^2+6s+5}\Big]\)
= 1/5 A.
8. A band-limited signal with a maximum frequency of 5 kHz is to be sampled. According to the sampling theorem, the sampling frequency which is not valid is _______________
a) 5 kHz
b) 12 kHz
c) 15 kHz
d) 20 kHz
View Answer
Explanation: (fs) min = 2 fm
Also, (fs) min = 2 X 5 = 10 kHz
So, fs ≥ 10 kHz.
9. A current I given by I = – 8 + 6\(\sqrt{2}\) (sin (ωt + 30°)) A is passed through three meters. The respective readings (in ampere) will be?
a) 8, 6 and 10
b) 8, 6 and 8
c) – 8, 10 and 10
d) -8, 2 and 2
View Answer
Explanation: PMMC instrument reads only DC value and since it is a centre zero type, so it will give – 8 values.
So, rms = \(\sqrt{8^2 + (\frac{6\sqrt{2}}{\sqrt{2}})^2)}\) = 10 A
Moving iron also reads rms value, so its reading will also be 10 A.
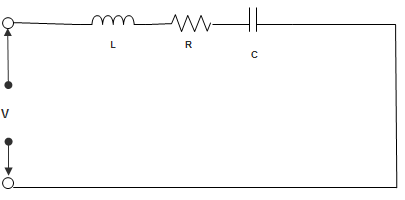
10. Given, R = 10 Ω, L = 100 mH and C = 10 μF. Selectivity is ____________
a) 10
b) 1.2
c) 0.15
d) 0.1
View Answer
Explanation: Selectivity = \(\frac{1}{Q}\)
Q = \(\frac{ωL}{R} = \frac{1000×100×10^{-3}}{10}\)
∴ Q = 10
So, Selectivity = 0.1.
11. Given that X(s) is the Laplace transform of the signal cos 2t u (t). The time signal corresponding to (s+1) X(s) is _________________
a) (cos 2t – 2 sin 2t) u (t)
b) (cos 2t + \(\frac{sin2t}{2}\)) u (t)
c) (cos 2t + 2 sin 2t) u (t)
d) (cos 2t – \(\frac{sin2t}{2}\)) u (t)
View Answer
Explanation: We know that, s X (s) + X(s) is having Laplace transform \(\frac{dx(t)}{dt}\) + x (t)
Or, y (t) = (cos 2t – 2 sin 2t) u (t).
12. Let x(t) be a continuous time, real valued signal band limited to F Hz. The Nyquist sampling rate in Hz, for y(t) = x(0.5t) + x(t) – x(2t) is ______________
a) F
b) 2F
c) 4F
d) 8F
View Answer
Explanation: Expansion in time domain is compression in frequency domain and vice versa. So, the maximum frequency component in given signal is 2F Hz. And according to sampling theorem,
Nyquist rate = 2 fm
= 2 X 2 F
= 4F Hz.
13. Increased pulse-width in the flat-top sampling , leads to ______________
a) Attenuation of high frequencies in reproduction
b) Attenuation of low frequencies in reproduction
c) Greater aliasing errors in reproduction
d) No harmful effects in reproduction
View Answer
Explanation: As pulse width T is increased, the width 1/T of the first lobe of the spectrum is decreased.
Hence, increased pulse-width in the flat-top sampling, leads to attenuation of high frequencies in reproduction.
14. A relay coil having voltage of magnitude 210 V and frequency 50 Hz is connected to a 210 V, 50 Hz supply. If it has resistance of 50 Ω and an inductance of 0.2 H, the apparent power is _____________
a) 549.39 VA
b) 275.6 VA
c) 157 VA
d) 187 VA
View Answer
Explanation: Z = 50 + j (0.2) (2π) (50) = 50 + 62.8
\(S = \frac{|V|^2}{Z} = \frac{210^2}{50-62.8}\)
Apparent Power |S| = \(\frac{210^2}{\sqrt{50^2 + 62.8^2}}\)
= 549.39 VA.
15. A band pass signal extends from 4-6 kHz. The smallest sampling frequency required to attain all the information in the signal is _________________
a) 10 kHz
b) 8 kHz
c) 6 kHz
d) 4 kHz
View Answer
Explanation: Upper cut-off frequency fH = 6 kHz
Bandwidth = 6k – 4k
= 2 kHz
Now, fs = \(\frac{2f_H}{k}\)
Where, k = \(\frac{f_H}{B}\)
= \(\frac{6 kHz}{2 kHz}\)
= 3
Also, fs = \(\frac{2 X 6 kHz}{3}\) = 4 kHz.
Sanfoundry Global Education & Learning Series – Signals & Systems.
To practice all areas of Signals & Systems, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
