This set of Signals & Systems Multiple Choice Questions & Answers (MCQs) focuses on “Properties of ROC”.
1. Given a system function H(s) = \(\frac{1}{s+3}\). Let us consider a signal sin 2t. Then the steady state response is ___________
a) \(\frac{1}{8}\)
b) Infinite
c) 0
d) 8
View Answer
Explanation: H(s) = \(\frac{V(s)}{J(s)}\)
= \(\frac{1}{s+3}\)
V(s) = \(\frac{1}{s+3}\). J(s)
J(s) = L (sin 2t) = \(\frac{2}{s^2+4}\)
V (s) = \(\frac{1}{s^2+4} . \frac{2}{s+3}\)
VSS = lims→0 sV(s)
= 0.
2. If H(f) = \(\frac{y(t)}{x(t)}\), then for this to be true x(t) is ___________
a) exp\((\frac{j2nf}{t})\)
b) exp\((-\frac{j2nf}{t})\)
c) exp(j2nft)
d) exp(-j2nft)
View Answer
Explanation: Let us consider x (t) = e2jnft
So, y (t) = \(\int_{-∞}^∞ h(τ)x(t-τ)dτ\)
= \(\int_{-∞}^∞ h(τ)e^{j2nπf(t-τ)} \,dτ\)
= ej2nft H (f)
Or, H (f) = \(\frac{y(t)}{e^{j2nft}}\)
So, x (t) = ej2nft.
3. The z-transform of –u(-n-1) is ___________
a) \(\frac{1}{1-z}\)
b) \(\frac{z}{1-z}\)
c) \(\frac{1}{1-z^{-1}}\)
d) \(\frac{z}{1-z^{-1}}\)
View Answer
Explanation: z [-u (-n-1)] = \(∑_{n=-1}^∞ [u(-n-1)] z^{-n}\)
= – [z + z2 + z3 + z4…]
= \(\frac{z}{z-1}\)
= \(\frac{1}{1-z^{-1}}\).
4. The value of z(ak u[-k]) is _______________
a) \(\frac{z}{z-a}\)
b) \(\frac{z}{a-z}\)
c) \(\frac{z^2}{z-a}\)
d) \(\frac{a}{a-z}\)
View Answer
Explanation: z (ak u [-k]) = \(∑_{k=-∞}^{-1} a^k z^{-k}\)
= \(∑_{m=1}^∞ a^{-m} z^m\)
= \(∑_{m=1}^∞ (a^{-1} z)^m \)
= \(\frac{a^{-1} z}{1-a^{-1} z} = \frac{z}{a-z}\).
5. If a system has N different poles, then the system can have ______________
a) N ROC’s
b) (N-1) ROC’s
c) (N+1) ROC’s
d) 2N ROC’s
View Answer
Explanation: Let us consider 2 poles. For 2 poles, we will have 3 ROC conditions. Hence, if a system has N poles then the system will have (N+1) ROC’s.
6. Given 2 signals (-3)k u(k) and u (k-1). These two signals are superimposed. This superimposed signal is _______________
a) \(\frac{z}{z+3} + \frac{1}{z-1}\)
b) \(\frac{z}{z+3} – \frac{1}{z-1}\)
c) \(\frac{z}{z-3} + \frac{1}{z-1}\)
d) \(\frac{z}{z+3} + \frac{1}{z+1}\)
View Answer
Explanation: We know that superposition means addition of these 2 signals.
So, superimposed f[k] = (-3)k u(k) + u(k-1)
Hence, z[k] = \(\frac{z}{z+3} + \frac{1}{z-1}\).
7. X1(z) = 2z + 1 + z-1 and X2(z) = z + 1 + 2z-1 is ________________
a) Even signal
b) Odd signal
c) In time power signal
d) In time energy signal
View Answer
Explanation: Given X1(z) = 2z + 1 + z-1 and X2(z) = z+1+2z-1.
So, x1(k) = {2, 1, 1}; x2(k) = {1, 1, 2}.
8. The value of z{[k-1] u(k)} is _______________
a) \(\frac{z(z+2)}{(z-1)^2}\)
b) \(\frac{2z-z^2}{(z-1)^2}\)
c) \(\frac{z^2}{(z-1)^2}\)
d) \(\frac{z(z-2)}{(z+1)^2}\)
View Answer
Explanation: z {[k-1] u (k)} = z {k u (k) – u (k)}
= \(\frac{z}{(z-1)^2} – \frac{z}{z-1}\)
= \(\frac{z-z(z-1)}{(z-1)^2}\)
= \(\frac{z-z^2+z}{(z-1)^2}\)
= \(\frac{2z-z^2}{(z-1)^2}\).
9. The area under Gaussian pulse \(\int_{-∞}^∞ e^{{-π}^{{t}^2}} \,dt \) is ___________
a) Unity
b) Infinity
c) Pulse
d) Zero
View Answer
Explanation: Putting \(π^{t^2}\) = x, we get,
\(\int_{-∞}^∞ e^{{-π}^{{t}^2}} \,dt = \int_{-∞}^∞ e^{-x} 2π \sqrt{\frac{x}{π}} \,dx\)
\(= 2\sqrt{π} \int_{-∞}^∞ \sqrt{x} e^{-x} \,dx\)
= 1.
10. The system x(k) = 7(\(\frac{1}{3}\))k u(-k-1)-6(\(\frac{1}{2}\))k u(k) is ___________
a) Causal
b) Anti-causal
c) Non-causal
d) Cannot be determined
View Answer
Explanation: Taking the z-transform, we get,
X (z) = \(7\left(\frac{1}{z-\frac{1}{3}}\right) – 6\left(\frac{1}{z-\frac{1}{2}}\right)\)
∴ the ROC for given condition is as derived above.
∴ the bounded signal as a whole is non-causal.
11. The spectral density of white noise is ____________
a) Exponential
b) Uniform
c) Poisson
d) Gaussian
View Answer
Explanation: The distribution of White noise is homogeneous over all frequencies. Power spectrum is the Fourier transform of the autocorrelation function. Therefore, the power spectral density of white noise is uniform.
12. In the circuit given below, the value of ZL for maximum power to be transferred is _____________
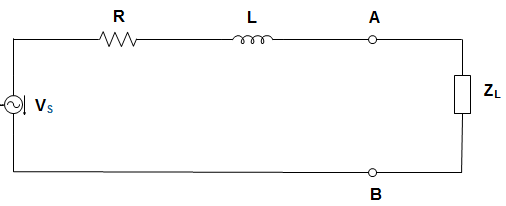
a) R
b) R + jωL
c) R – jωL
d) jωL
View Answer
Explanation: The value of load for maximum power transfer is given by the complex conjugate of ZAB
ZAB = R + jXL
= R + jωL
∴ ZL for maximum power transfer is given by ZL = R – jωL.
13. A current I given by I = – 8 + 6\(\sqrt{2}\) (sin (ωt + 30°)) A is passed through three meters. The respective readings (in ampere) will be?
a) 8, 6 and 10
b) 8, 6 and 8
c) – 8, 10 and 10
d) -8, 2 and 2
View Answer
Explanation: PMMC instrument reads only DC value and since it is a center zero type, so it will give – 8 values.
So, rms = \(\sqrt{8^2 + (\frac{6\sqrt{2}}{\sqrt{2}})^2}\) = 10 A
Moving iron also reads rms value, so its reading will also be 10 A.
14. The CDF for a certain random variable is given as F(x) = {0, -∞<x≤0; kx2, 0<x≤10; 100k, 10<x<∞;} The value of k is __________
a) 100
b) 50
c) 1/50
d) 1/100
View Answer
Explanation: From the given F(x),
We get, \(\frac{dF(x)}{dx}\) = 0 + 2kx + 0
= 2kx
∴ \(\int_0^{10}\) 2 kx dx =1
Or, 100k = 1
Or, k = 1/100.
15. For a stable system which of the following is correct?
a) |z| < 1
b) |z| = 1
c) |z| > 1
d) |z| ≠ 1
View Answer
Explanation: We know that, for the system to be stable, the ROC should include the unit circle.
|z| = 1, represents the unit circle but does not include it.
|z| > 1, represents the region outside the unit circle. In other words, it excludes the region of the unit circle.
|z| ≠ 1 does not represent a unit circle.
Sanfoundry Global Education & Learning Series – Signals & Systems.
To practice all areas of Signals & Systems, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
