This set of Signals & Systems Multiple Choice Questions & Answers (MCQs) focuses on “Periodic and Non-Periodic Signals”.
1. Given the signal
X (t) = cos t, if t<0
Sin t, if t≥0
The correct statement among the following is?
a) Periodic with fundamental period 2π
b) Periodic but with no fundamental period
c) Non-periodic and discontinuous
d) Non-periodic but continuous
View Answer
Explanation: From the graphs of cos and sin, we can infer that at t=0, the function becomes discontinuous.
Since, cos 0 = 1, but sin 0 = 0
As 1 ≠ 0, so, the function X (t) is discontinuous and therefore Non-periodic.
2. The fundamental period of the signal X (t) = 10 cos2(10 πt) is __________
a) 0.2
b) 0.1
c) 0.5
d) No fundamental period exists
View Answer
Explanation: X (t) = 10 cos2 (10 πt)
Since, cos 2t = 2cos2 t – 1
Or, cos2 t = \(\frac{1+cos2t}{2}\)
∴ X (t) = 5 + 5 cos 20πt
Now, Y (t) = cos 20πt
Fundamental period of the signal is = \(\frac{2π}{20π} = \frac{1}{10}\) = 0.1.
3. The even component of the signal X (t) = ejt is _________________
a) Sin t
b) Cos t
c) Sinh t
d) Cosh t
View Answer
Explanation: Let Xe (t) represents the even component of X (t)
Now, Xe (t) = \(\frac{1}{2}\)[X (t) + X (-t)]
= \(\frac{1}{2}\)[ejt + e-jt]
= cos t.
4. The odd component of the signal X (t) = ejt is _______________
a) Sin t
b) Cos t
c) Sinh t
d) Cosh t
View Answer
Explanation: Let Xo (t) represents the odd component of X (t)
Now, Xo (t) = \(\frac{1}{2}\)[X (t) – X (-t)]
= \(\frac{1}{2}\)[ejt + e-jt]
= sin t.
5. The period of the signal X (t) = 24 + 50 cos 60πt is _______________
a) \(\frac{1}{30}\) s
b) 60 π s
c) \(\frac{1}{60π}\) s
d) Non-periodic
View Answer
Explanation: Period of cos t = 2π
Period of cos at = \(\frac{2π}{a}\)
Here, a = 60π
So, period of cos 60πt = \(\frac{2π}{60π}\)
= \(\frac{1}{30}\) s.
6. The period of the signal X (t) = 10 sin 5t – 4 cos 9t is _______________
a) \(\frac{24π}{35}\)
b) \(\frac{4π}{35}\)
c) 2π
d) Non-periodic
View Answer
Explanation: Period of cos t = 2π
Period of cos at = \(\frac{2π}{a}\)
Here, a = 9
So, period of cos 9t = \(\frac{2π}{9}\)
Again, Period of sin t = 2π
Period of sin at = \(\frac{2π}{a}\)
Here, a = 5
So, period of sin 5t = \(\frac{2π}{5}\)
∴ Period of X (t) = LCM [Period of X1 (t), Period of X2 (t)]
∴ Period of X (t) = LCM (\(\frac{2π}{5}, \frac{2π}{9}\)) = 2π.
7. The period of the signal X (t) = 5t – 2 cos 6000 πt is ________________
a) 0.96 ms
b) 1.4 ms
c) 0.4 ms
d) Non-periodic
View Answer
Explanation: Period of cos t = 2π
Period of cos at = \(\frac{2π}{a}\)
Here, a = 6000π
So, period of cos 6000πt = \(\frac{2π}{6000π}\)
= \(\frac{1}{3000}\)
Again, Period of t = indefinite
∴ Period of X (t) = LCM [Period of X1 (t), Period of X2 (t)]
∴ Period of X (t) = LCM (\(\frac{1}{3000}\), ∞) = Indefinite.
8. The period of the signal X (t) = 4 sin 6t + 3 sin \(\sqrt{3}\)t is ________________
a) \(\frac{2π}{3}\) s
b) \(\frac{2π}{\sqrt{3}}\) s
c) 2π s
d) Non-periodic
View Answer
Explanation: Period of sin t = 2π
Period of sin at = \(\frac{2π}{a}\)
Here, a = 6
So, period of sin 6t = \(\frac{2π}{6}\)
Again, a = \(\sqrt{3}\)
So, period of sin \(\sqrt{3}\)t = \(\frac{2π}{\sqrt{3}}\)
∴ Period of X (t) = LCM [Period of X1 (t), Period of X2 (t)]
∴ Period of X (t) = LCM (\(\frac{π}{3}, \frac{2π}{\sqrt{3}}\)) = Indefinite.
9. The period of the signal Z (t) = sin3t + cos 4t is _______________
a) periodic without a definite period
b) periodic with a definite period
c) non- periodic over an interval
d) non-periodic throughout
View Answer
Explanation: Period of cos t = 2π
Period of cos at = \(\frac{2π}{a}\)
Here, a = 4
So, period of cos 4t = \(\frac{2π}{4}\)
= \(\frac{π}{2}\)
Again, Period of sin t = 2π
Period of sin at = \(\frac{2π}{a}\)
Here, a = 3
So, period of sin 3t = \(\frac{2π}{3}\)
∴ Period of X (t) = LCM [Period of X1 (t), Period of X2 (t)]
∴ Period of X (t) = LCM (\(\frac{2π}{5}, \frac{2π}{4}\)) = definite
Hence Z (t) is periodic with a definite period.
10. The signal X (t) = e-4t u (t) is _______________
a) Power signal with P∞ = \(\frac{1}{4}\)
b) Power signal with P∞ = 0
c) Energy signal with E∞ = \(\frac{1}{4}\)
d) Energy signal with E∞ = 0
View Answer
Explanation: If a signal has E∞ as ∞ and P∞ as a finite value, then the signal is a power signal. If a signal has E∞ as a finite value and P∞ as ∞, then the signal is an energy signal.
|x (t)| < ∞, E∞ = \(\int_{-∞}^∞ |x(t)|^2 \,dt\)
= \(\int_∞^∞ e^{-4t} u(t) \,dt \)
= \(\in_∞^∞ e^{-4t} \,dt = \frac{1}{4}\)
So, this is not a power signal but an energy signal.
\(P_∞ = lim_{T→∞} \frac{1}{2T} \int_{-T}^T |x(t)|^2 \,dt = ∞.\)
11. The signal X (t) = \(e^{j(2t + \frac{π}{6})}\) is ________________
a) Power signal with P∞ = 1
b) Power signal with P∞ = 2
c) Energy signal with E∞ = 2
d) Energy signal with E∞ = 1
View Answer
Explanation: If a signal has E∞ as ∞ and P∞ as a finite value, then the signal is a power signal. If a signal has E∞ as a finite value and P∞ as ∞, then the signal is an energy signal.
|x (t)| = 1, E∞ = \(\int_{-∞}^∞ |x(t)|^2 \,dt = ∞\)
So, this is a power signal not an energy signal.
\(P_∞ = lim_{T→∞} \frac{1}{2T} \int_{-T}^T |x(t)|^2 \,dt = 1.\).
12. Signal X (t) is as shown in the figure below.
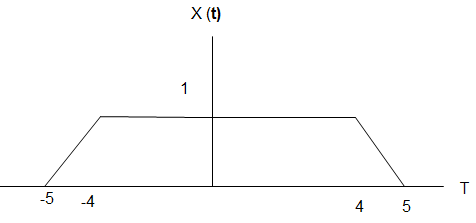
The total energy of X (t) is _______________
a) 0
b) 13
c) \(\frac{13}{3}\)
d) \(\frac{26}{3}\)
View Answer
Explanation: E = 2\(\int_0^5 x^2 (t) \,dt\)
= 2 \(\int_0^4 1^1 \,dt + 2\int_4^5 (5 – t^2) \,dt\)
= 8 + \(\frac{2}{3} = \frac{26}{3}\).
13. A discrete time signal is as given below
\(X [n] = cos \frac{πn}{9} + sin (\frac{πn}{7} + \frac{1}{2})\)
The period of the signal X [n] is ______________
a) 126
b) 32
c) 252
d) Non-periodic
View Answer
Explanation: Given that, N1 = 18, N2 = 14
We know that period of X [n] (say N) = LCM (N1, N2)
∴ Period of X [n] = LCM (18, 14) = 126.
14. A discrete time signal is as given below
\(X [n] = cos (\frac{n}{8}) cos (\frac{πn}{8})\)
The period of the signal X [n] is _____________
a) 16 π
b) 16(π+1)
c) 8
d) Non-periodic
View Answer
Explanation: We know that for X [n] = X1 [n] × X2 [n] to be periodic, both X1 [n] and X2 [n] should be periodic with finite periods.
Here X2 [n] = cos (\(\frac{πn}{8}\)), is periodic with fundamental period as \(\frac{8}{n}\)
But X1 [n] = cos (\(\frac{n}{8}\)) is non periodic.
∴ X [n] is a non-periodic signal.
15. A discrete time signal is as given below
\(X [n] = cos (\frac{πn}{2}) – sin (\frac{πn}{8}) + 3 cos (\frac{πn}{4} + \frac{π}{3})\)
The period of the signal X [n] is _____________
a) 16
b) 4
c) 2
d) Non-periodic
View Answer
Explanation: Given that, N1 = 4, N2 = 16, N3 = 8
We know that period of X [n] (say N) = LCM (N1, N2, N3)
∴ Period of X [n] = LCM (4, 16, 8) = 16.
Sanfoundry Global Education & Learning Series – Signals & Systems.
To practice all areas of Signals & Systems, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
