Signals & Systems Questions and Answers – Convolution : Impulse Response Representation for LTI Systems – 2

fracThis set of Signals & Systems Questions and Answers for Campus interviews focuses on “Convolution : Impulse Response Representation for LTI Systems – 2”.

1. The convolution sum is given by _____ equation.
a) x[n]*h[n] = \(∑_{k=-∞}^∞\) x[k]h[n-k]
b) x[n]*h[n] = \(∑_{k=-∞}^∞\) x[n]h[n-k]
c) x[n]*h[n] = \(∑_{k=-∞}^∞\) x[k]h[k]
d) x[n]*h[n] = \(∑_{k=-∞}^∞\) x[k]h[-k]
View Answer

2. When the sequences x1 [n] = u [n] and x2 [n] = u [n-3], the output of LTI system is given as _____
a) y[n] = n-2, n>3
b) y[n] = n-2, n≥3
c) y[n] = n+2, n>3
d) y[n] = n-2, n≤3
View Answer

Answer: b
Explanation: The output y[n] =∑^∞_k=-∞u(k)u(n-k-3), by solving the above summation either by graphically or by direct summation we get .

3. The impulse response h (t) of an LTI system is given by e^-2t.u(t) . What is the step response?
a) y(t) = ¹⁄₂ (1 – e^-2t) u (t)
b) y(t) = ¹⁄₂ (1 – e^-2t)
c) y(t) = (1- e^-2t) u (t)
d) y(t) = ¹⁄₂ (e^-2t) u (t)
View Answer

Answer: a
Explanation: Given x (t) = u (t) and h (t) = e^-2t.u(t). By using convolution integral

We get output y (t) as y(t) = ¹⁄₂ (1 – e^-2t) u (t).

4. Is (t)*h(t) = h(t)*x(t)?
a) True
b) False
View Answer

Answer: a
Explanation: By the properties of convolution we say that x(t)*h(t) = h(t)*x(t)
It can be proved using the convolution integral
.

5. Compute u (t) convolved with itself?
a) y(t)=t.u(t)
b) y(t)=u(t)
c) y(t)=t².u(t)
d) y(t)=t.u(t-1)
View Answer

Answer: a
Explanation: By taking x (t) = u (t) and h (t) = u (t) and substituting in the integral
On solving the given integral we get y (t) = t u (t).

6. Convolve the signals e^-2t u(t), e^-3t u(t). Determine the output?
a) y(t) = (e^-2t – e^-3t)u(t)
b) y(t) = (e^-2t – e^-3t)
c) y(t) = (e^-3t – e^-2t)u(t)
d) y(t) = (e^-t – e^-3t)u(t)
View Answer

Answer: a
Explanation: By solving the convolution integral
, we get output asy(t) = (e^-2t – e^-3t)u(t).

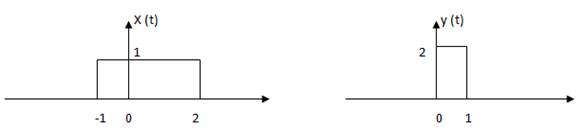
7. Convolve graphically.

a)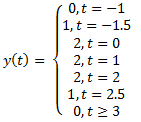
b)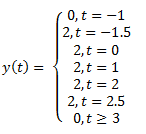
c)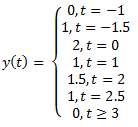
d)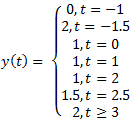
View Answer

Answer: a
Explanation: Step 1: sketch x (τ) and h (-τ)
Step 2: Obtain the product x (τ) h (t-τ) and the area under this product will give y (0)
Step 3: sketch h (1-τ) and compute y (1) and so on
Step 4: similarly sketch h (-1-τ) and compute y (-1) and so on.
Hence we get the output as .

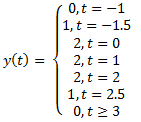8. Convolve graphically the below given signals, and determine the correct sequence?

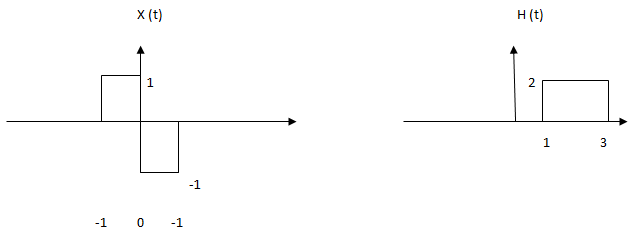
a) Y (-1) = 0, y (1) = 2, y (3) = 2
b) Y (-1) = 2, y (1) = 2, y (3) = 2
c) Y (-1) = 0, y (1) = 0, y (3) = 2
d) Y (-1) = 0, y (1) = 3, y (3) = 2
View Answer

Answer: a
Explanation: Step 1: sketch x (τ) and h (-τ)
Step 2: Obtain the product x (τ) h (t-τ) and the area under this product will give y (0)
Step 3: sketch h (1-τ) and compute y (1) and so on
Step 4: similarly sketch h (-1-τ) and compute y (-1) and so on.
By following above steps we get the output as

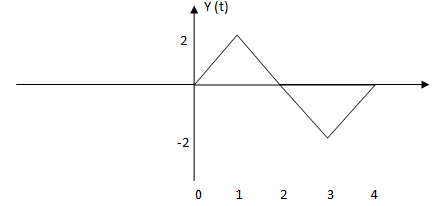
9. Convolve given x (t) with itself and choose the correct output.

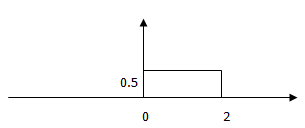
a)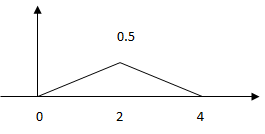
b)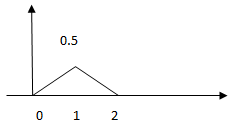
c)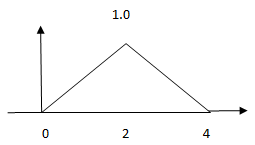
d)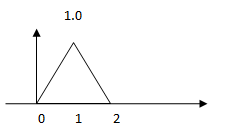
View Answer

10. Find the convolution of x1[n] = {1, 2, 3, 4} and x2[n] = {2, 1, 2, 1}.
a) Y[n] = {14, 10, 14, 10}
b) Y [n] = {14, 16, 14, 16}
c) Y [n] = {14, 16,-14,-16}
d) Y [n] = {14,-16,-14, 16}
View Answer

Sanfoundry Global Education & Learning Series – Signals & Systems.

To practice all areas of Signals & Systems for Campus Interviews, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]