This set of Signals & Systems Questions and Answers for Experienced people focuses on “Elementary Signals – 2”.
1. Mathematical representation of given rectangular pulse is ______
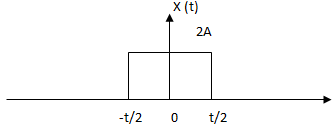
a) X (t) = {2A, t/2 < 0 < -t/2
b) X (t) = {2A, -t/2 < 0 < t/2
c) X (t) = {2A, 0 <= |t| <= t/2
{0, |t| > t/2
d) X (t) = {2A, 0 <|t| < t/2
{0, |t| > t/2
View Answer
Explanation: The given rectangular pulse is of amplitude 2A for the time interval –t/2 to t/2 and zero otherwise.
2. If ![X [n] will be of amplitude for the interval 0 to 4 & zero otherwise](https://www.sanfoundry.com/wp-content/uploads/2018/07/signals-systems-questions-answers-experienced-q2.png){kind=small}
describe x [n] as superposition of two step functions.
a) X [n] = u [n] – u [n-5].
b) X [n] = u [n] + u [n-5].
c) X [n] = u [n-5] – u [n].
d) X [n] = u [n-5] + u [n].
View Answer
Explanation: X [n] will be of amplitude for the interval 0 to 4 and zero otherwise. It can be obtained by the equation x [n] = u [n] – u [n-5].
3. Discrete-time version of unit impulse is defined as ______
a) ∂ [n] = \(\bigg\{\begin{matrix}
1, & n=0\\
0, & n≠0
\end{matrix}\)
b) ∂ [n] = \(\bigg\{\begin{matrix}
1, & n≠0\\
0, & n=0
\end{matrix}\)
c) ∂ [n] = { 1, for all n
d) ∂ [n] = \(\bigg\{\begin{matrix}
A, & n=0\\
0, & n≠0
\end{matrix}\)
View Answer
Explanation: Unit impulse is an elementary signal with zero amplitude everywhere except at n = 0.
4. Which of the following is not true about unit impulse function?
a) ∂ [n] = \(\bigg\{\begin{matrix}
1, & n=0\\
0, & n≠0
\end{matrix}\)
b) ∂(t)=0, for t≠0
c) \(\int_{-∞}^∞\) ∂(t)dt=1
d) \(\int_{-∞}^∞\) ∂(t)dt=0
View Answer
Explanation: One option gives the definition of discrete-time version of impulse function, other options give continuous-time representation of impulse function.
5. The step function u (t) is integral of _______ with respect to time t.
a) Ramp function
b) Impulse function
c) Sinusoidal function
d) Exponential function
View Answer
Explanation: Step function is an integral of impulse function and conversely, impulse is the derivative of step function u (t).
6. The area under the pulse defines _____ of the impulse.
a) Strength
b) Energy
c) Power
d) Duration
View Answer
Explanation: The area under the pulse defines strength of the impulse and the strength of the impulse is denoted by the label next to the arrow.
7. Unit impulse ∂(t) is _____ of time t.
a) Odd function
b) Even function
c) Neither even nor odd function
d) Odd function of even amplitude
View Answer
Explanation: For an impulse function, ∂(-t)= ∂(t). Hence unit impulse is an even function of time t.
8. Shifting property of impulse ∂(t) is given by ______
a) \(\int_{-∞}^∞\) x(t) ∂(t-to) dt=x(to)
b) \(\int_{-∞}^∞\) x(t) ∂(t-to) dt=x(t)
c) \(\int_{-∞}^∞\) x(t-to) ∂(t) dt=x(to)
d) \(\int_{-∞}^∞\) x(t) ∂(t-to) dt=∂(to)
View Answer
Explanation: X (t) be a function and the product of x (t) with time shifted delta function ∂(t – to) gives x(to), this is referred to as shifting property of impulse function.
9. ∂(at) = 1⁄a ∂(t), this property of unit impulse is called ______
a) Time shifting property
b) Time scaling property
c) Amplitude scaling property
d) Time reversal property
View Answer
Explanation: Impulse function exhibits shifting property, time scaling property. And time scaling property is given by∂(at) = 1⁄a ∂(t).
10. Which of the following is not true about the ramp function?
a) 
b) r (t) = t u (t)
c) Ramp function with unit slope is integral of unit step
d) Integral of unit step is a ramp function of unit slope
View Answer
Explanation: The impulse function is derivative of the step function. In the same way the integral of step function is a ramp function of unit slope.
∫u(t) = r(t).
Sanfoundry Global Education & Learning Series – Signals & Systems.
To practice all areas of Signals & Systems for Experienced people, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
