This set of Signals & Systems Multiple Choice Questions & Answers (MCQs) focuses on “Discrete Fourier Transform”.
1. Given that S1 and S2 are two discrete time systems. Consider the following statements:
i) If S1 and S2 are linear, then S is linear
ii) If S1 and S2 are non-linear, then S is non-linear
iii) If S1 and S2 are causal, then S is causal
iv) If S1 and S2 are time invariant, then S is time invariant
The true statements from the above are ____________
a) i, ii, iii
b) ii, iii, iv
c) I, iii, iv
d) I, ii, iii, iv
View Answer
Explanation: Only statement ii is false.
For example, S1: y[n] = x[n] +b and S2: y[n] = x[n]-b, where, b≠0.
S{x[n]} = S2 {S1{x[n]}} = S2{x[n] +b} = x[n]
Hence, S is linear.
2. For two discrete time systems, consider the following statements:
i) If S1 and S2 are linear and time invariant, then interchanging their order does not change the system.
ii) If S1 and S2 are linear and time variant, then interchanging their order does not change the system
The correct statement from the above is __________
a) Both i & ii
b) Only i
c) Only ii
d) Neither i, nor ii
View Answer
Explanation: S1: y[n] = n x[n]
And S2: y[n] = n x [n+1]
If x[n] = δ[n], then S2 {S1 {δ[n]}} = S2 [0] = 0
S1 {S2 {δ[n]}} = S1 {δ[n+1]} = – δ[n+1]≠0.
3. The following input-output pairs have been observed during the operation of a time invariant system
i) x1[n] = {1, 0, 2} (Laplace transform) y1 [n] = {0, 1,2}
ii) x2[n] = {0,0, 3} (Laplace transform) y2[n] = {0,1,0,2}
iii) x3[n] = {0,0,0,1} (Laplace transform) y3[n] = {1,2,1}
The conclusion regarding the linearity of the system is _____________
a) Linear
b) Non-linear
c) One more observation is required
d) Conclusion cannot be drawn from observation
View Answer
Explanation: System is not linear. This is evident from the observation of the pairs, x3[n] – y3[n] and x2[n] and y2[n]. If the system were linear y2[n] would be of the form y2[n] = {3, 6, 3}.
4. S1 and S2 are two DT systems which are connected together to form a new system. Consider the following statements:
i) If S1 and S2 are non-causal, then S is non-causal
ii) If S1 and/or S2 are unstable, then S is unstable
The correct statement from the above is ____________
a) Both i and ii
b) Only i
c) Only ii
d) Neither i nor ii
View Answer
Explanation: S1: y[n] = x [n+1] …… (Non-causal)
S2: y[n] = x [n-2] ……… (Causal)
S: y[n] = x [n-1] which is causal ………. (False)
S1: y[n] = ex[n] stable, S2: y[n] = ln(x[n]) ……… (Unstable)
But S: y[n] = x[n] ………. (Stable, false)
5. Given a signal x[n] = δ[n] + 0.9 δ [n − 6]. The Discrete Time Fourier Transform for 8 points is __________
a) 1 – 0.9 \(e^{-j \frac{2π}{8} k6}\)
b) 1 + 0.9 \(e^{-j \frac{2π}{8} k6}\)
c) 1 + 0.9 \(e^{j \frac{2π}{8} k6}\)
d) 1 – 0.9 \(e^{j \frac{2π}{8} k6}\)
View Answer
Explanation: Given N = 8.
Now, x[k] = \(∑_0^{N-1} x[n] e^{-j \frac{2π}{N} kn}\)
= \(∑_0^7 x[n] e^{-j \frac{2π}{8} kn}\)
= \(∑_{N=0}^7 (δ[n] + 0.9 δ [n – 6])e^{-j \frac{2π}{8} kn}\)
= 1 + 0.9 \(e^{-j \frac{2π}{8} kn}\)
Here, n = 6, from given question.
Hence, x[k] = 1 + 0.9 \(e^{-j \frac{2π}{8} k6}\).
6. The Z transform of δ (n − m) is ___________
a) z-n
b) z-m
c) \(\frac{1}{z-n}\)
d) \(\frac{1}{z-m}\)
View Answer
Explanation: δ (n − m) is a delayed impulse function which is delayed by m units. We know that the Z-transform of a delayed function f (n-m) is (z-m) times the Z-transform of the function f (n). So, the Z transform of δ (n − m) is z-m.
7. A 10 V is connected across a load whose V-I characteristics is given by 7I = V2 + 2V. The internal resistance of the battery is of magnitude 1Ω. The current delivered by the battery is ____________
a) 6 A
b) 5 A
c) 7 A
d) 8 A
View Answer
Explanation: 7I = V2 + 2V …………………. (1)
Now, V = 10 – 1 × I
Putting the value of V in eqt (1), we get,
&I = (10 – I) 2 + 2(10 – I) …………………. (2)
Or, I = 100 + I2 – 20I + 20 – 2I
Or, I2 – 29I + 120 = 0
∴ \(I = \frac{+29 ± \sqrt{29^2 – 4(120)}}{2} = \frac{29 ± 19}{2}\)
I = 5 A, 24 A
Now, I = 24 A is not possible because V will be negative from eqt (2)
∴ I = 5 A.
8. The period of the signal x(t) = 10 sin 12 π t + 4 cos18 π t is ____________
a) \(\frac{π}{4}\)
b) \(\frac{1}{6}\)
c) \(\frac{1}{9}\)
d) \(\frac{1}{3}\)
View Answer
Explanation: There are two waveforms of frequencies 6 and 9, respectively. Hence the combined frequency is the highest common factor between 6 and 9 which is 3. Therefore the period is \(\frac{1}{3}\).
9. Given a series RLC circuit with V = 5V, R = 200 kΩ, C = 10µF. Sampling frequency of the circuit is 10 Hz. The expression and the ROC of the z-transform of the sampled signal are ____________
a) \(\frac{5z}{z-e^{-5′}}\), |z|<e-5
b) \(\frac{5z}{z-e^{-0.05′}}\), |z|<e-0.05
c) \(\frac{5z}{z-e^{-0.05′}}\), |z|>e-0.05
d) \(\frac{5z}{z-e^{-5′}}\), |z|>e-5
View Answer
Explanation: I (t) = \(\frac{V}{R} e^{-t/RC}\)
Voltage across resistor = R I (t)
= V e-t/RC = 5 e-t/RC
= 5 \(e{\frac{-t}{200 × 10 × 10^{-6} × 10^3}}\) = 5 e-t/2
Given that, the Sampling frequency of the circuit = 10 Hz
Hence, x (n) = 5e-n/2 X 10 = 5e-0.05n
Now, X (z) = \(∑_{n=-∞}^∞ x[n]z^{-n}\)
= 5 \(∑_{n=-∞}^∞ (e^{-0.05} z^{-n})^n\)
= 5. \(\frac{1}{1-e^{-0.05} Z^{-1′}}\), ROC |z|>e-0.05
= \(\frac{5z}{z-e^{-0.05′}}\), |z|>e-0.05.
10. Given a series RLC circuit with V = 5V, R = 200 kΩ, C = 10µF. Sampling frequency of the circuit is 10 Hz. The samples x (n), where n=0,1,2,…., is ___________
a) 5(1-e-0.05n)
b) 5e-0.05n
c) 5(1-e-5n)
d) 5e-5n
View Answer
Explanation: The charging current in circuit I (t) = I (0+) e-t/RC
Since the capacitor acts as short circuit, I (0+) = \(\frac{V}{R}\)
∴ I (t) = \(\frac{V}{R}\) e-t/RC
Voltage across resistor = R I (t)
= V e-t/RC = 5 e-t/RC
= 5 \(e{\frac{-t}{200 × 10 × 10^{-6} × 10^3}}\) = 5 e-t/2
Given that, the Sampling frequency of the circuit is 10 Hz
∴ x (n) = 5e-n/2 X 10 = 5e-0.05n.
11. For the circuit given below, if the frequency of the source is 50 Hz, then a value of to which results in a transient free response is _________________
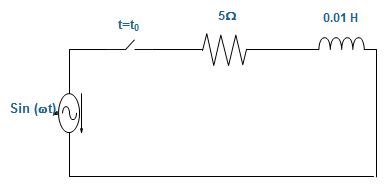
a) 0
b) 1.78 ms
c) 7.23 ms
d) 9.21 ms
View Answer
Explanation: T = \(\frac{L}{R} \)
Or, T = \(\frac{0.01}{5}\) = 0.002 s = 2 ms
For the ideal case, transient response will die out with time constant.
Practically, T will be less than 2 ms.
12. If G(f) represents the Fourier Transform of a signal g (t) which is real and odd symmetric in time, then G (f) is ____________
a) Complex
b) Imaginary
c) Real
d) Real and non- negative
View Answer
Explanation: Fourier transform of g (t) is G (f)
Given that, g (t) is real, odd and symmetric with respect to time.
∴G*(jm) = – G(jm); G(jm) purely imaginary.
13. If R1 is the region of convergence of x (n) and R2 is the region of convergence of y(n), then the region of convergence of x (n) convoluted y (n) is ___________
a) R1 + R2
b) R1 – R2
c) R1 ∩ R2
d) R1 ∪ R2
View Answer
Explanation: The z-transform of x (n) = X (z). Let the region of convergence be R1
The z-transform of y (n) = y (z). Let the region of convergence be R2
The z-transform of x (n) * y (n) is X (z).Y (z) [from property]
So, the region of convergence is R1 ∩ R2.
14. The system under consideration is an RC low-pass filter with R = 1 kΩ and C = 1 µF. Let H (f) denotes the frequency response of the RC, low-pass filter. Let f1 be the highest frequency, such that 0≤|f|≤f1, \(\frac{|H(f1)|}{H(0)}\)≥0.95 Then f1 is ___________
a) 327.8
b) 163.9
c) 52.2
d) 104.4
View Answer
Explanation: H (ω) = \(\frac{\frac{1}{jωC}}{R+(\frac{1}{jωC})} = \frac{1}{1+jωRC}\)
H (f) = \(\frac{1}{1+j2πfRC}\)
|H (f)| = \(\frac{1}{\sqrt{1+4π^2 f_1^2 R^2 C^2}}\)
H (0) = 1
Given that \(\frac{|H(f1)|}{H(0)}\)≥0.95
Or, 1 + 4π2 f12 R2 C2 ≤ 1.108
Simplifying, f1 ≤ \(\frac{0.329}{2πRC}\)
∴f1 ≤ 52.2 Hz.
15. The response of the LTI system for \(\frac{d^2 y(t)}{dt^2} + \frac{dy(t)}{dt} + 5y(t) = \frac{dx(t)}{dt}\). Given that y(0–) = 2, \(\frac{dx(t)}{dt}\) (at t=0) = 0, x(t) = u(t) is __________
a) 2e-t cos t u(t)
b) 0.5 e-t sin t u(t)
c) 2e-t cos t u(t) + 0.5 e-t sin t u(t)
d) 0.5 e-t cos t u(t-1) + 2e-t sin t u(t-1)
View Answer
Explanation: s2Y(s) – 2s + 2sY(s) – 2 + 5Y(s) = 1
∴ (s2+2s+5) Y(s) = 3+2s
Or, Y(s) = \(\frac{2s+3}{s^2+2s+5}\)
= \(\frac{2(s+1)}{(s+1)^2 + 2^2} + \frac{1}{(s+1)^2 + 2^2}\)
Hence, y (t) = 2e-t cos t u(t) + 0.5 e-t sin t u(t).
Sanfoundry Global Education & Learning Series – Signals & Systems.
To practice all areas of Signals & Systems, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
