This set of Signals & Systems Interview Questions and Answers for freshers focuses on “Basic Operations on Signals – 2”.
1. Considering Figure 1, sketch y= 2* x (t).
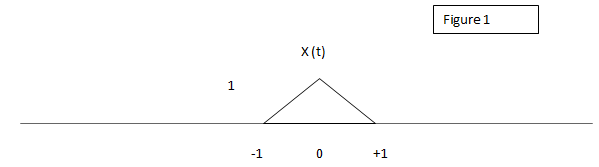
a)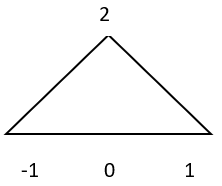 
b)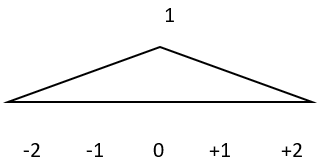 
c)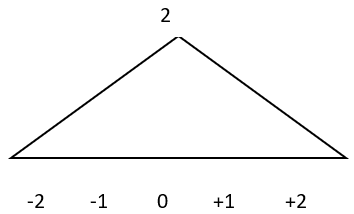 
d)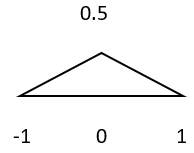 
View Answer
Explanation: Y (t) = 2*x (t) is an example for amplitude scaling. Here amplitude is scaled by a factor 2.
2. Considering Figure 1, sketch y= -3* x (t).
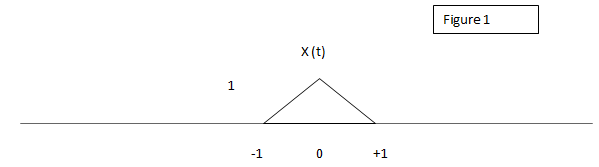
a)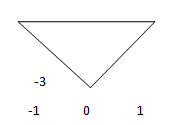
b)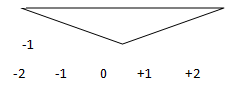
c)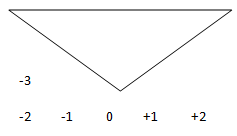
d)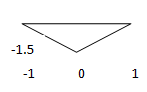
View Answer
Explanation: Y (t) = -3*x (t) is an example for amplitude scaling. Here amplitude is scaled by a factor -3.
3. In the following diagram, X [n] and y [n] are related by ______
![X [n] & y [n] are related by Y [n] = 2*x [n] in the following diagram](https://www.sanfoundry.com/wp-content/uploads/2018/07/signals-systems-interview-questions-answers-freshers-q3.png)
a) Y [n] = 2*x [n]
b) Y [n] = -2*x [n]
c) Y [n] = x [2n]
d) Y [n] = x [-2n]
View Answer
Explanation: Y [n] = 2*x [n] is an example for amplitude scaling of discrete time signal. The given figure is an example for 2*x [n] hence Y [n] = 2*x [n] is correct.
4. X [n] and y [n] is as shown below, the relationship between x [n] and y [n] is given by ______
![The relationship between x [n] & y [n] is given by Y [n] = x [n]/3](https://www.sanfoundry.com/wp-content/uploads/2018/07/signals-systems-interview-questions-answers-freshers-q4.png)
a) X [n] = y [n]/3
b) X [n] = 3* y [n]
c) Y [n] = x [n]/3
d) Y [n] = 3*x [n]
View Answer
Explanation: The given y [n] is amplitude scaling of a discrete time signal by a factor 1/3.
Hence the amplitude is reduced by 1/3.
5. Considering figure 3 below, is the following figure true for y [n] = x [2n]?
![Find the following figure for y [n] = x [2n]](https://www.sanfoundry.com/wp-content/uploads/2018/07/signals-systems-interview-questions-answers-freshers-q5.png)
![X [2n] is an example of time scaling for discrete time signal x [k*n]](https://www.sanfoundry.com/wp-content/uploads/2018/07/signals-systems-interview-questions-answers-freshers-q5a.png)
a) True
b) False
View Answer
Explanation: X [2n] is an example of time scaling. For discrete time signal x [k*n], k>1 the samples will be lost.
6. Considering figure 3 below, is the following figure true for y [n] = x [n/2]?
![X [n/2] is an example for time scaling by factor 1/2 & it will be a stretched signal](https://www.sanfoundry.com/wp-content/uploads/2018/07/signals-systems-interview-questions-answers-freshers-q6.png)
a) True
b) False
View Answer
Explanation: X [n/2] is an example for time scaling by factor ½ and it will be a stretched signal. The discrete time signal should extend from -10 to 10.
7. Consider figure 4, is the given y (t) an integration of x (t)?
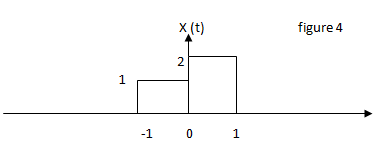
a) Y (t) = ∫x (t).dt
b) Y (t) = ∫x2 (t).dt
c) Y (t) = 3* ∫x (t).dt
d) Y (t) = 3* ∫x2 (t).dt
View Answer
Explanation: The given y (t) is integral of x (t) and amplitude 3 remains constant for t>1.
It is because of the properties of integration.
8. Consider figure 4, is the given y (t) a differentiation of x (t)?
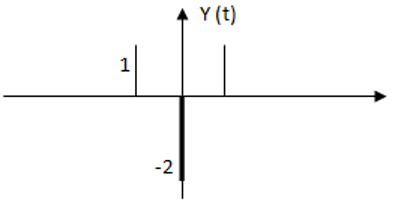
a) Y (t) = \(\frac{dx(t)}{dt}\)
b) Y (t) = \(\frac{-2dx(t)}{dt}\)
c) Y (t) = \(\frac{dx(-t)}{dt}\)
d) Y (t) = ∫x (t).dt
View Answer
Explanation: The given y (t) is differentiation of x (t) and hence we have impulses at -1, 0 and 1.
9. The given pair x (t) and y (t) is _______
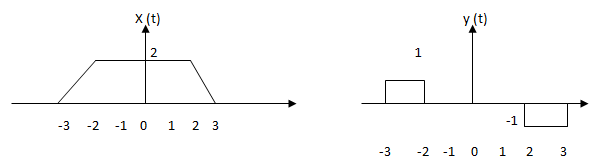
a) Y (t) = d/dt (x (t))
b) Y (t) = ∫x (t).dt
c) Y (t) = x (t) -1
d) Y (t) = x (t) /2
View Answer
Explanation: The given pair x (t) and y (t) is related by y (t) = d/dt (x (t)). From -2 to 2 we have Y (t) is zero because differentiation of constant is zero.
10. The given pair x (t) and y (t) is related by _______
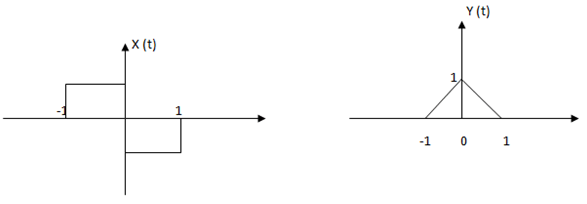
a) Y (t) = d/dt (x (t))
b) Y (t) = x (t) + 1
c) Y (t) = ∫x (t) .dt
d) Not related
View Answer
Explanation: The given pair x (t) and y (t) is related by Y (t) = ∫x (t) .dt. The integral of x (t) gives the Y (t). Y (t) = 0 for t > 1.
Sanfoundry Global Education & Learning Series – Signals & Systems.
To practice all areas of Signals & Systems for Interviews, here is complete set of 1000+ Multiple Choice Questions and Answers.
