This set of Neural Networks Multiple Choice Questions & Answers (MCQs) focuses on “Neural Networks – Cost Function”.
1. Which of the following statements is not true about the cost function?
a) It is a measure of how good a neural network did with respect to its given training sample and the expected output
b) It depend on variables such as weights
c) It is a single value, not a vector
d) It never depends on bias
View Answer
Explanation: A cost function is a measure of how good a neural network did with respect to its given training sample and the expected output. It depends on variables such as weights and biases. A cost function is a single value, not a vector, because it rates how good the neural network did as a whole.
2. Which of the following is not a cost function requirement?
a) The cost function must be able to be written as an average
b) The cost function must not be dependent on any activation values of a neural network
c) Technically a cost function can be dependent on any output values
d) If the cost function is dependent on other activation layers besides the output one, back propagation will be valid
View Answer
Explanation: Technically a cost function can be dependent on any output values. And it just makes this restriction so that we can backpropagate. If the cost function is dependent on other activation layers besides the output one, back propagation will be invalid because the idea of trickling backwards no longer works.
3. When the cost function increases, the learning rate also increases.
a) True
b) False
View Answer
Explanation: When you define a cost function for a neural network, the goal is to minimize this cost function. Cost function does not converge to an optimal solution and can even diverge. If the cost oscillates wildly, the learning rate is too high. So if the cost increases, the learning rate is too high.
4. Which of the following statements is not true about cost function?
a) Cost function is also called a loss or error function
b) Its goal is to maximize the cost function
c) We want to define a cost function to find the weight in the neural network
d) It wants different cost functions for regression and classification problems
View Answer
Explanation: Cost function is also called a loss or error function. Our goal is to minimize the cost function and not to maximize it. We want to define a cost function to find the weight in the neural network. And we want different cost functions for regression and classification problems.
5. A variational problem is one in which we are looking for a function which can optimize a certain cost function.
a) True
b) False
View Answer
Explanation: Variational problems can also be expressed and solved numerically using back propagation networks. A variational problem is one in which we are looking for a function which can optimize a certain cost function. Usually cost is expressed analytically in terms of the unknown function and finding a solution is in many cases an extremely difficult problem.
6. Mean squared error is a simple and commonly used cost function.
a) True
b) False
View Answer
Explanation: Mean squared error is a simple and commonly used cost function and it is given as C = \(\frac {1}{n}\)∑\(_{i=1} ^{n}\)(yi – yi‘)2, where y is the expected output and y‘ is the actual predicted output. Cost function gives a value which we want to optimize and there are so many other cost functions.
7. Very mall learning rate improves cost function.
a) True
b) False
View Answer
Explanation: The learning rate cannot be too small because many more iterations will be required to reach the minimum where the actual goal is to minimize the cost function. A better idea is to select the dynamic learning rate which decreases over time because it allows the algorithm to swiftly identify the point.
8. The cost function of a neural network is always convex.
a) True
b) False
View Answer
Explanation: The cost function of a neural network J (W, b) is in general neither convex nor concave. This means that the matrix of all second partial derivatives \(\frac {\partial J}{\partial W}\) (the Hessian) is neither positive semidefinite, nor negative semidefinite. Since the second derivative is a matrix, it’s possible that it’s neither one nor the other.
9. Which of the following statements is not true about the cost function?
a) The maximum of the concave function is a point where the derivative is 0
b) The maximum of the convex function is a point where the derivative is 0
c) Analytical Approach is used to find out the minimum or maximum of a cost function
d) Hill climbing approach is used to find out the minimum or maximum of a cost function
View Answer
Explanation: The minimum of the convex function and the maximum of a concave function is a point where the derivative is 0. Analytical Approach and Hill climbing approach are the two methods to find out the minimum or maximum of a cost function.
10. The below figure shows a convex function.
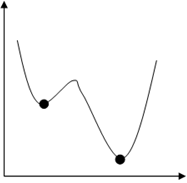
a) True
b) False
View Answer
Explanation: Generally, our goal is to optimize the cost function. And the figure shows a non convex function. Functions like sigmoid function are non-convex function which means that there are multiple local minimums as shown in the figure. So, it’s not guaranteed to converge to the global minimum.
11. Given the cost function C(hθ (x), y) = \(\begin{cases} -log (h_{\theta} (x)) & if \, y = 1 \\
– log (1 – h_{\theta} (x)) & if \, y = 0 \\
\end{cases}
\) is used to make gradient descent algorithm, to be able to find the global minimum.
a) True
b) False
View Answer
Explanation: The given cost function is a log function which is used to make gradient descent algorithm, to be able to find the global minimum. In case where labeled value y is equal to 1 the hypothesis is –log (h(x)) or –log (1-h(x)) otherwise. And we are only interested in the (0, 1) x-axis interval since hypothesis can only take values in that range.
12. What is the cost function from the following data by using MSE?
| Expected output | 15 | 17 | 10 | 26 | 14 | 12 | 11 | 13 |
| Actual output | 12 | 19 | 15 | 24 | 13 | 14 | 8 | 11 |
a) 5.5
b) 6.5
c) 7.5
d) 8.5
View Answer
Explanation: Mean squared error is a type of cost function. C = \(\frac {1}{n}\)∑\(_{i=1} ^{n}\)(yi – yi‘)2, where y is the expected output and y‘ is the actual predicted output.
Cost function, C = \(\frac {1}{8}\) ((15 – 12)2 + (17 – 19)2 + (10 – 15)2 + (26 – 24)2 + (14 – 13)2 + (12 – 14)2 + (11 – 8)2 + (13 – 11)2
= \(\frac {1}{8}\) (9 + 4 + 25 + 4 + 1 + 4 + 9 + 4)
= \(\frac {60}{8}\)
= 7.5
Sanfoundry Global Education & Learning Series – Neural Networks.
To practice all areas of Neural Networks, here is complete set on 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
