This set of Neural Networks Multiple Choice Questions & Answers (MCQs) focuses on “Backpropagation Algorithm – Set 3″.
1. What will be the values of net input of h1 and net input of h2 from the below figure, given that w1 = 0.2, w2 = 0.15, w3 = 0.3, w4 = 0.25, w5 = 0.45, w6 =0.4, w7 = 0.55, w8 = 0.5?
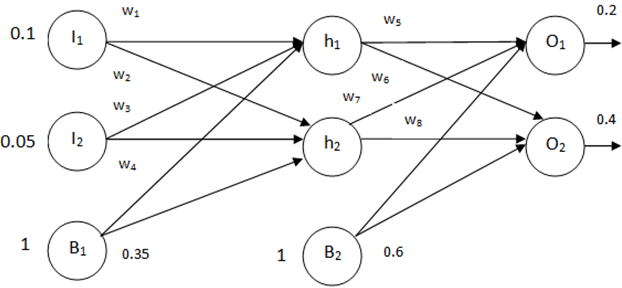
a) 0.385, 0.378
b) 0.358, 0.682
c) 0.853, 0.387
d) 0.583, 0.826
View Answer
Explanation: Given w1 = 0.2, w2 = 0.15, w3 = 0.3, w4 = 0.25, w5 = 0.45, w6 =0.4, w7 = 0.55, w8 = 0.5, I1 = 0.1, I2 = 0.05, B1 = 0.35 and B2 = 0.6.
We have net input h1 = I1 * w1 + I2 * w3 + 1 * B1
= 0.1 * 0.2 + 0.05 * 0.3 + 1 * 0.35
= 0.02 + 0.015 + 0.35
= 0.385
net input h2 = I1 * w2 + I2 * w4 + 1 * B1
= 0.1 * 0.15 + 0.05 * 0.25 + 1 * 0.35
= 0.015 + 0.013 + 0.35
= 0.378
2. What will be the outputs of h from the below figure, given that the net input h1 = 0.38 and net input h2 = 0.37 using the logistic function?

a) 0.514, 0.511
b) 0.594, 0.591
c) 0.494, 0.525
d) 0.454, 0.256
View Answer
Explanation: Given the net input h1 = 0.38 and net input h2 = 0.37. Using the logistic function to get the output of h1:
Out h1 = \(\frac {1}{1+ e^{-net \, h_1}}\)
= \(\frac {1}{1+ e^{-0.38}}\)
= \(\frac {1}{1+ 0.684}\)
= 0.594
Out h2 = \(\frac {1}{1+ e^{-net \, h_2}}\)
= \(\frac {1}{1+ e^{-0.37}}\)
= \(\frac {1}{1+ 0.691}\)
= 0.591
3. What will be the net inputs of the output layer in the below figure, given that the w5 = 0.45, w6 =0.4, w7 = 0.55, w8 = 0.5, Out h1 = 0.6 and Out h2 = 0.65?

a) 1.628, 1.365
b) 1.228, 1.165
c) 1.528, 1.665
d) 1.428, 1.465
View Answer
Explanation: Given w5 = 0.45, w6 =0.4, w7 = 0.55, w8 = 0.5, Out h1 = 0.6, Out h2 = 0.65 and B2 = 0.6.
We have net input O1 = Out h1 * w5 + Out h2 * w7 + 1 * B2
= 0.6 * 0.45 + 0.65 * 0.55 + 1 * 0.6
= 0.27 + 0.358 + 0.6
= 1.228
net input O2 = Out h1 * w6 + Out h2 * w8 + 1 * B2
= 0.6 * 0.4 + 0.65 * 0.5 + 1 * 0.6
= 0.24 + 0.325 + 0.6
= 1.165
4. What will be the outputs of output layer from the below figure, given that the net input O1 = 1.3 and net input O2 = 1.41 using the logistic function?

a) 0.867, 0.408
b) 0.876, 0.048
c) 0.768, 0.084
d) 0.786, 0.804
View Answer
Explanation: Given the net O1 = 1.3 and net O2 = 1.41. Using the logistic function to get the output of h1
Out O1 = \(\frac {1}{1+ e^{-net \, O_1}}\)
= \(\frac {1}{1+ e^{-1.3}}\)
= \(\frac {1}{1+ 0.273}\)
= 0.786
Out O2 = \(\frac {1}{1+ e^{-net \, O_2}}\)
= \(\frac {1}{1+ e^{-1.41}}\)
= \(\frac {1}{1+ 0.244}\)
= 0.804
5. What will be the total error of the given neural network given output values O1 and O2 are 0.63 and 0.78 respectively?

a) 0.093
b) 0.2
c) 0.165
d) 0.072
View Answer
Explanation: Given the output Out O1 = 0.63, Out O2 = 0.78. And from the figure target O1 = 0.2 and target O2 = 0.4.
Error O1 = \(\frac {1}{2}\)(target O1 – Out O1)2
= \(\frac {1}{2}\)(0.2 – 0.63)2
= \(\frac {1}{2}\)(-0.43)2
= \(\frac {1}{2}\) * 0.185
= 0.093
Error O2 = \(\frac {1}{2}\)(target O2 – Out O2)2
= \(\frac {1}{2}\)(0.4 – 0.78)2
= \(\frac {1}{2}\)(-0.38)2
= \(\frac {1}{2}\) * 0.144
= 0.072
Errortotal = Error O1 + Error O2
= 0.093 + 0.072
= 0.165
6. Given the below neural network with Out O1 = 0.15 and Out O2 = 0.25. How much does the total error change with respect to the outputs?

a) 0.2, 0.4
b) 0.75, 0.55
c) 0.35, 0.25
d) 0.72, 0.38
View Answer
Explanation: Given the output Out O1 = 0.55, Out O2 = 0.65. And from the figure target O1 = 0.2 and target O2 = 0.4.
Errortotal = \(\frac {1}{2}\)(target O1 – Out O1)2 + \(\frac {1}{2}\)(target O2 – Out O2)2
\(\frac {\partial E_{total} }{\partial Out \, O_1}\) = – (target O1 – Out O1) (Basic derivation)
= – (0.2 – 0.55)
= 0.35
\(\frac {\partial E_{total}}{\partial Out \, O_2}\) = – (target O2 – Out O2) (Basic derivation)
= – (0.4 – 0.65)
= 0.25
7. Given the below neural network with w5 = 0.4, Output h1 = 0.57 and Output h2 = 0.55. How much does the total net input of O1 changes with respect to w5?

a) 0.4
b) 0.45
c) 0.55
d) 0.57
View Answer
Explanation: Given the w5 = 0.4, Output h1 = 0.57 and Output h2 = 0.55.
\(\frac {\partial net \, O_1}{\partial w_5}\) = Out h1 * w5 + Out h2 * w7 + 1 * B2
net O1w5 = Out h1 (Basic derivation)
= 0.57
8. How much does the output of O1 change with respect to its total net input, given the Out O1 = 0.31 (using logistic function) in the below figure?

a) 0.31
b) 0.214
c) 0.691
d) 0.524
View Answer
Explanation: We know, Out O1 = \(\frac {1}{1+ e^{-net \, O_1}}\)
\(\frac {\partial Out \, O_1}{\partial net \, O_1}\) = Out O1 (1 – Out O1) (Basic derivation)
= 0.31 (1 – 0.31)
= 0.31 * 0.69
= 0.214
9. Given the below neural network with w5 = 0.4, Output O1 = 0.5 and Out h1 = 0.59. How much does the total error changes with respect to w5?

a) 0.044
b) 0.25
c) 0.3
d) 0.59
View Answer
Explanation: Given w5 = 0.4, Output O1 = 0.5, Out h1 = 0.59 and target O1 = 0.2. As we have to calculate the total error changes with respect to w5: \(\frac {\partial E_{total}}{\partial w_5} = \frac {\partial E_{total}}{\partial Out \, O_1} * \frac {\partial Out \, O_1}{\partial net \, O_1} * \frac {\partial net \, O_1}{\partial w_5}\)
\(\frac {\partial E_{total}}{\partial w_5}\) = (– (target O1 –Out O1) )* (Out O1 (1 – Out O1)) * (Out h1)
= – (0.2 – 0.5) * 0.5 * (1 – 0.5) * 0.59
= – (– 0.3) * 0.5 * 0.5 * 0.59
= 0.3 * 0.25 * 0.59
= 0.044
10. What will be the new value of w5 in the below figure, given w5 = 0.4, total error changes with respect to w5= 0.08 and learning rate = 0.5?

a) 0.5
b) 0.4
c) 0.36
d) 0.8
View Answer
Explanation: Given w5 = 0.4, total error changes with respect to w5, \(\frac {\partial E_{total}}{\partial w_5} \) = 0.08 and learning rate η = 0.5.
w5new = w5 – η * \(\frac {\partial E_{total}}{\partial w_5} \)
= 0.4 – 0.5 * 0.08
= 0.4 – 0.04
= 0.36
Sanfoundry Global Education & Learning Series – Neural Networks.
To practice all areas of Neural Networks, here is complete set on 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
