This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “Matching”.
1. Which of the following refers to a set of edges with no shared endpoints?
a) Dominating set
b) Matching
c) Independent set
d) Cut edge
View Answer
Explanation: In a simple graph G, a matching or any edge set in a graph, is a set of edges with no vertices in common. It can also be an entire graph consisting of edges with no common vertices. Hence, matching refers to a set of edges with no shared endpoints.
2. In a perfect matching of graph G, every vertex is connected to how many edges?
a) At most one
b) At least one
c) Exactly one
d) Zero
View Answer
Explanation: In a graph G, perfect matching is said to be the matching, that saturates every vertex of the graph. It is a maximal matching set such that it induces the degree of all the vertices as exactly one. Every perfect matching is a maximal matching set.
3. In a graph G, the total number of edges in maximum matching is called?
a) Matching number
b) Chromatic number
c) Domination number
d) Independence number
View Answer
Explanation: In a graph G, maximum matching is a matching of maximum size among all matchings in the graph. It is also known as the largest maximal matching. The cardinality of the maximum matching set is the matching number.
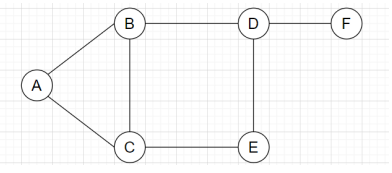
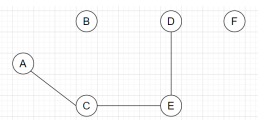
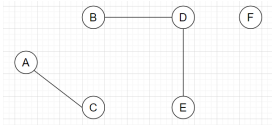
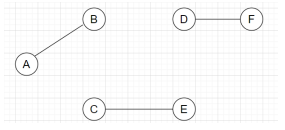
4. Which of the following refers to the perfect matching for the graph given below?
a)
b)
c)
d)
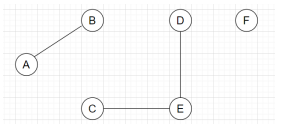
View Answer
Explanation: In a graph G, a perfect matching is a maximal matching set such that it induces the degree of all the vertices as exactly one. Hence, from all the given graphs, the graph with degree of all the vertices as 1 and covering all the vertices of the graph will be an appropriate perfect matching.
5. In a graph, perfect matching exists only if the number of vertices is even.
a) True
b) False
View Answer
Explanation: In a graph G, perfect matching saturates every vertex of the graph. All the vertices are to be covered in it. So the number of edges in perfect matching is half the number of vertices. Hence, perfect matching exists if the number of vertices is even.
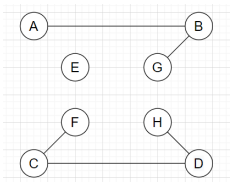
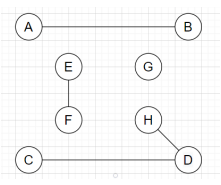
6. Which of the following refers to the maximal matching graph for the graph given below?
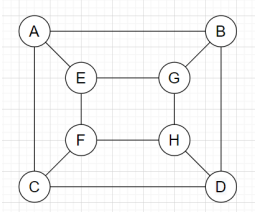
a)
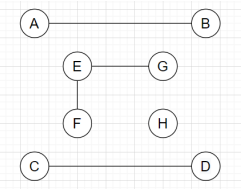
b)
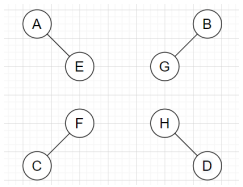
c)
d)
View Answer
Explanation: In a graph, maximal matching means a matching of maximal cardinality, which cannot be increased by adding any edge. If we add any edge to the graph, it violates the matching of the graph. Hence, from all the given graphs, the graph which doesn’t violates the matching by adding any vertex will be an appropriate maximal matching.
7. In a graph, every maximum matching is a maximal matching.
a) True
b) False
View Answer
Explanation: A maximal matching in a graph is a matching, which cannot be increased by adding any edge and a maximum matching is a matching of maximum size among all matchings in the graph. Hence, we can say that the given statement is correct.
8. Which among the following is an application of graph matching?
a) Traveling salesperson problem
b) Graph coloring
c) Knapsack problem
d) Maximum subset problem
View Answer
Explanation: One of the applications of graph matching is graph coloring. In graph coloring, all the vertices of the graph are labeled with colors, such that two adjacent vertices do not share the same color. Apart from vertex coloring, it is used in scheduling, flow networks, stable marriage problem and many more.
Sanfoundry Global Education & Learning Series – Data Structures & Algorithms.
To practice all areas of Data Structures & Algorithms, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Data Structure MCQ
- Practice Computer Science MCQs
- Check Programming Books
- Check Design and Analysis of Algorithms Books
- Check Computer Science Books
