This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “Vertex Cover Problem”.
1. Vertex covering can be a good approach to which type of the problems?
a) Where all the vertex in the graph need to be included
b) Where all the edges in the graph need to be included
c) Only half edges in the graph need to be included
d) Only half of the total vertices need to be included
View Answer
Explanation: A vertex cover is a subset of the vertex set of a given graph G, such that every edge in G is incident to at least one endpoint in the set. Hence, the vertex covering can be a good approach, where all the edges in the graph need to be included.
2. The greedy algorithm can find a minimal vertex cover in polynomial time for which among the following?
a) Tree graphs
b) Bipartite graphs
c) Hypercube
d) Clique graphs
View Answer
Explanation: Despite the NP-completeness of the problems, the konigs theorem allows the bipartite vertex problem to be solved in polynomial time, for bipartite graphs. Hence, the greedy algorithm can find a minimum vertex cover in polynomial time for bipartite graphs.
3. What is the minimum vertex cover for the following graph given below?
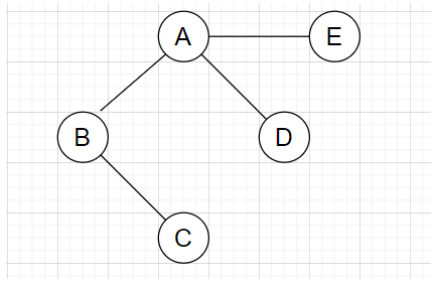
a) {A, B}
b) {A, E}
c) {B, C}
d) {D, B}
View Answer
Explanation: According to the given graph, the greedy approach can be followed: First, find a vertex v with maximum degree. Add the vertex to the solution and remove the vertex and its incident edges from the graph. Repeat for all the edges present in the graph. Hence, we can observe that node A has a maximum degree, so it can cover maximum edges. It covers the edge {A, B}, {A, D} and {A, E} and the rest {B, C} can be covered by including B or C in the resultant set. Hence, {A, B} or {A, C} is the minimum vertex cover for the following graph
4. Given below is the pseudocode of the vertex cover problem. Which of the following best suits the blank?
Vertex_Cover(G = (V, E))
{
A = { }
while (E!=0)
{
pick any edge (u, v) from E
add u and v to A
________________
}
return A
}a) remove every edge incident on either u or v
b) add every edge incident on u
c) delete the vertex
d) delete adjacent edge
View Answer
Explanation: First of all, initialize an empty set A which will store the results. Let V, E be the number of vertices and edges present in the graph. While E is not empty, pick any random edge from the set E and add it to the resultant set A. If any edge is incident on either u or v, remove that edge and return the resultant set.
5. In a complete bipartite graph Km, n, the minimum vertex cover is of the size max{m, n}.
a) True
b) False
View Answer
Explanation: In a complete bipartite graph Km, n, all the vertices of one side are connected to all the vertices of another side. Hence, the minimum number of edges can be covered by selecting the minimum number of vertices present on any of the sides.
6. Consider a simple graph G with 18 vertices. What will be the size of the maximum independent set of G, if the size of the minimum vertex cover of G is 10?
a) 8
b) 18
c) 28
d) 10
View Answer
Explanation: By removing the vertex cover vertices from the graph it results in an isolated graph, and so the remaining vertices would be the independent set in the original graph. Hence, size of maximum independent set = 18 – 10 = 8.
7. If the complement of a graph is an independent set, then the set of vertices itself is a vertex cover.
a) True
b) False
View Answer
Explanation: An independent set is a vertex subset such that no edge exists between any two in the subset. Whereas a vertex subset is a vertex cover if and only if its complement is an independent set. Hence, the given statement is true.
8. Which among the following problem uses the vertex cover approach?
a) Traveling salesperson problem
b) Assignment problem
c) Activity selection problem
d) Knapsack problem
View Answer
Explanation: A traveling salesperson problem refers to the problem where salespersons visit all the cities to sell their goods. They know the distance between all the cities. Hence, to decide the order in which they should visit the cities to minimize their travel time, a vertex cover approach can be used.
Sanfoundry Global Education & Learning Series – Data Structures & Algorithms.
To practice all areas of Data Structures & Algorithms, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Programming MCQs
- Practice Data Structure MCQ
- Practice Computer Science MCQs
- Apply for Computer Science Internship
- Check Design and Analysis of Algorithms Books
