Karger's Algorithm Questions and Answers

This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “Karger’s Algorithm”.

1. Which of the following algorithm can be used to find the minimum cut of a connected graph?
a) Fleury’s algorithm
b) Hirschberg’s algorithm
c) Karger’s algorithm
d) Hierholzer’s algorithm
View Answer

Answer: c
Explanation: In a given undirected and unweighted graph, the Karger’s algorithm can be used to find the minimum cut of the graph. It gives the minimum number of edges, on the removal of whose the graph gets disconnected into two different components.

2. Karger’s algorithm is which type of algorithm?
a) brute force algorithm
b) divide and conquer algorithm
c) greedy algorithm
d) randomized algorithm
View Answer

Answer: d
Explanation: Randomized algorithms are characterized by their random behavior. For better efficiency in all cases including the average case, we randomly select all the possible outcomes. In Karger’s algorithm, we randomly choose the edges. Hence, randomness plays a huge role in its implementation and it is a randomized algorithm.

3. On removal of which of the following edges gives the minimum cut for the graph given below?

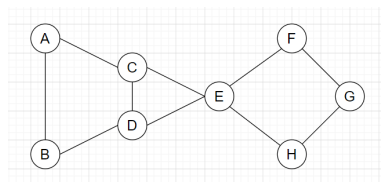
a) A-B, C-D
b) C-D, F-G
c) C-E, D-E
d) E-F, G-H
View Answer

Answer: c
Explanation: Minimum cut is the removal of a set of edges, in such a way that it makes the graph disconnected in two different components. From the given option, removing the edge C-E and D-E will make the graph disconnected in two different components.

4. Consider the following algorithm of Karger’s algorithm given below. Which of the following best suits the blank?

Let G=(V, E)
while (V > 2)
  pick any edge e from E randomly
  __________________________
  remove self-loops
return the cut left with last 2 vertices

a) merge or contract both vertices in a single vertex
b) delete the edge
c) delete both the vertex connected to it
d) contract the connected vertices
View Answer

Answer: a
Explanation: In a graph G with V vertices and E edges, pick up any edge from the graph and merge both the connected vertices into a single vertex and keep changing the graph accordingly. Remove all the self-loops from the graph and return when the graph is left with the last two final vertices.

Note: Join free Sanfoundry classes at Telegram or Youtube

5. Karger’s algorithm always gives a minimum cut for a connected graph.
a) True
b) False
View Answer

Answer: b
Explanation: Karger’s algorithm gives the minimum cut of a connected graph with the success probability of greater than or equal to 1/(n²). Suppose there are 5 nodes in a graph, the probability that it gives the minimum cut is only 1/25. Hence, Karger’s algorithm doesn’t always give the minimum cut for a connected graph.

6. The success probability of Karger’s algorithm can be increased.
a) True
b) False
View Answer

Answer: a
Explanation: The success probability of Karger’s algorithm to find the minimum cut of a connected graph is only 1/(n²), where n is the number of nodes in the graph. By running the basic algorithm repeatedly and returning the minimum cuts found, the success probability of Karger’s algorithm can be increased.

7. Which of the following best represents the time complexity of Karger’s algorithm?
a) O(n)
b) O(1)
c) O(n²)
d) O(log n)
View Answer

Answer: c
Explanation: The Karger’s algorithm to find the minimum cut, if the graph uses adjacency list or adjacency matrix, the implementation of edge contractions can be done with linear updates in the adjacency list or adjacency matrix. Hence, it takes O(n²) time, where n is the number of nodes in the graph.

8. Which of the following is an application of the minimum cut problem?
a) Pre-order traversal
b) To find strongly connected components
c) To study the reliability of a network
d) Detecting cycle in a graph
View Answer

Answer: c
Explanation: The minimum cut problem of a graph minimizes the sum of the weights of the edges crossing the partition. To find whether the network is reliable or not, the concept of minimum cut can be used. It detects the smallest number of edges that may fail in the network.

Sanfoundry Global Education & Learning Series – Data Structures & Algorithms.

To practice all areas of Data Structures & Algorithms, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Chromatic Number Multiple Choice Questions and Answers (MCQs)

» Next - Edge Coloring Multiple Choice Questions and Answers (MCQs)

Related Posts:

Recommended Articles: